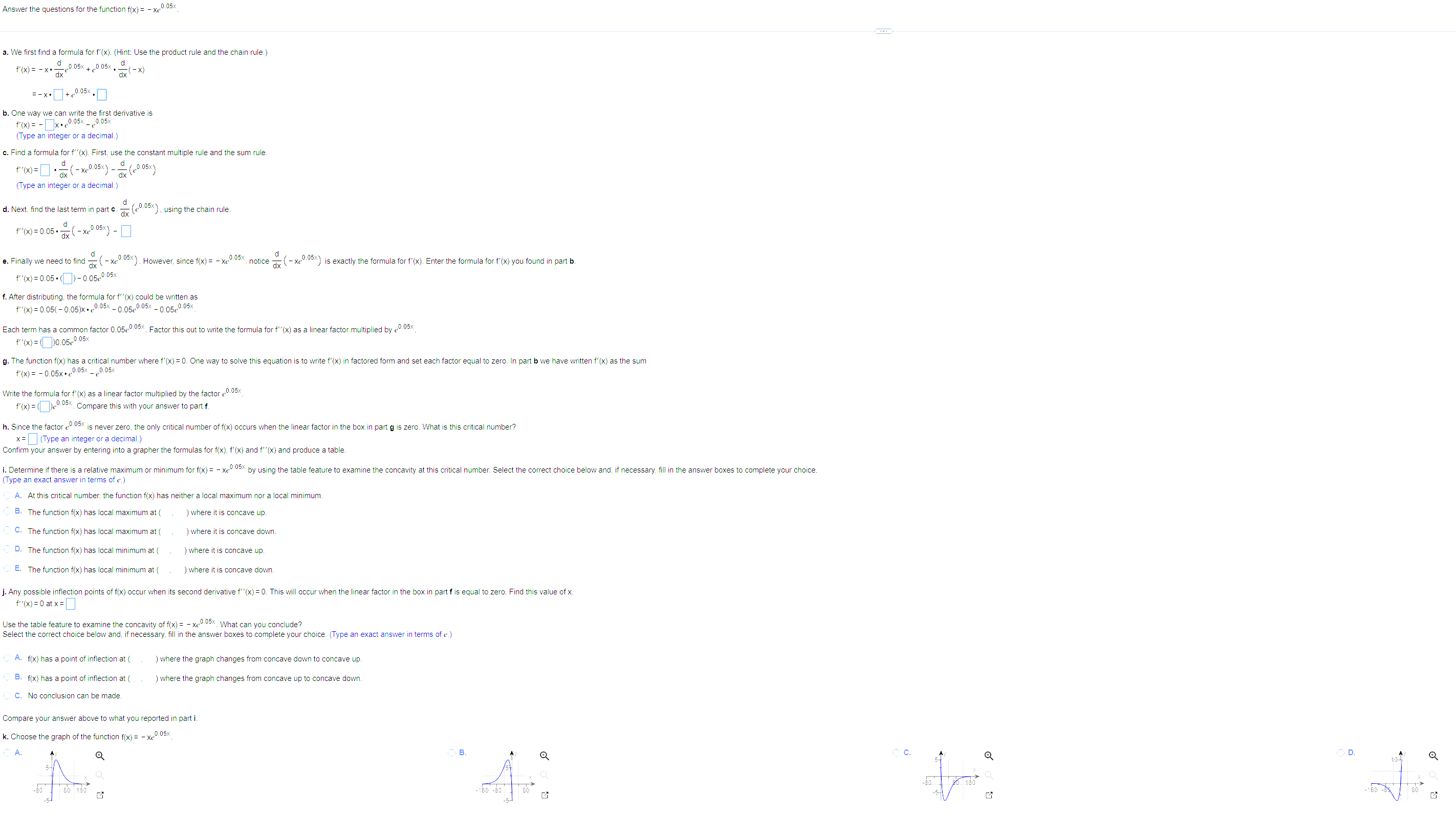
Answer the questions for the function f(x) = - xe0.05x . We first find a formula for f'(x). (Hint: Use the product rule and the chain rule.) f' (x) = -x. .0.05x + 0.05x . -( = -x.]+ 0.05x . b. One way we can write the first derivative is f'(x)= - x . 0 05x _ 0.05x (Type an integer or a decimal.) c. Find a formula for f"(x). First, use the constant multiple rule and the sum rule. 1. (-xe 0.05x ) -( f"'(x) =] . ax(- (Type an integer or a decimal.) d. Next, find the last term in part c. dy (0.05x ) , using the chain rule. f'(x)= 0.05 . ax ( -xe0.05x) - e. Finally we need to find ay ( - xe0.05x) . However, since f(x) = - xe0.05%, notice ax ( -xe0.05x) is exactly the formula for f'(x). Enter the formula for f'(x) you found in part b. f'(x) = 0.05 . ()- 0.050.05x f. After distributing, the formula for f"(x) could be written as f"(x) = 0.05( - 0.05)x . 0.05x - 0.050.05x - 0.050.05x Each term has a common factor 0.050.05%. Factor this out to write the formula for f"(x) as a linear factor multiplied by e.05x. f''(x) = ( )0.050.05x g. The function f(x) has a critical number where f'(x) = 0. One way to solve this equation is to write f'(x) in factored form and set each factor equal to zero. In part b we have written f'(x) as the sum f'(x) = - 0.05x . 0.05x _ 0.05x Write the formula for f'(x) as a linear factor multiplied by the factor 0.05x f'(x) =(). Compare this with your answer to part f. . Since the factor @ :05x is never zero, the only critical number of f(x) occurs when the linear factor in the box in part g is zero. What is this critical number? *= (Type an integer or a decimal.) Confirm your answer by entering into a grapher the formulas for f(x), f'(x) and f"(x) and produce a table . Determine if there is a relative maximum or minimum for f(x) = - xe * by using the table feature to examine the concavity at this critical number. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. Type an exact answer in terms of e.) A. At this critical number, the function f(x) has neither a local maximum nor a local minimum. B. The function f(x) has local maximum at ( ) where it is concave up C. The function f(x) has local maximum at ( ) where it is concave down. D. The function f(x) has local minimum at ( ) where it is concave up E. The function f(x) has local minimum at ( ) where it is concave down. j. Any possible inflection points of f(x) occur when its second derivative f"(x) = 0. This will occur when the linear factor in the box in part f is equal to zero. Find this value of x. f"'(x) =0 at x = Use the table feature to examine the concavity of f(x) = - xe :05%. What can you conclude? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. (Type an exact answer in terms of e.) A. f(x) has a point of inflection at ( )where the graph changes from concave down to concave up. B. f(x) has a point of inflection at ( ) where the graph changes from concave up to concave down. C. No conclusion can be made Compare your answer above to what you reported in part i. k. Choose the graph of the function f(x) = - xe0.05x A B 160