answer to 34

solve 35 please

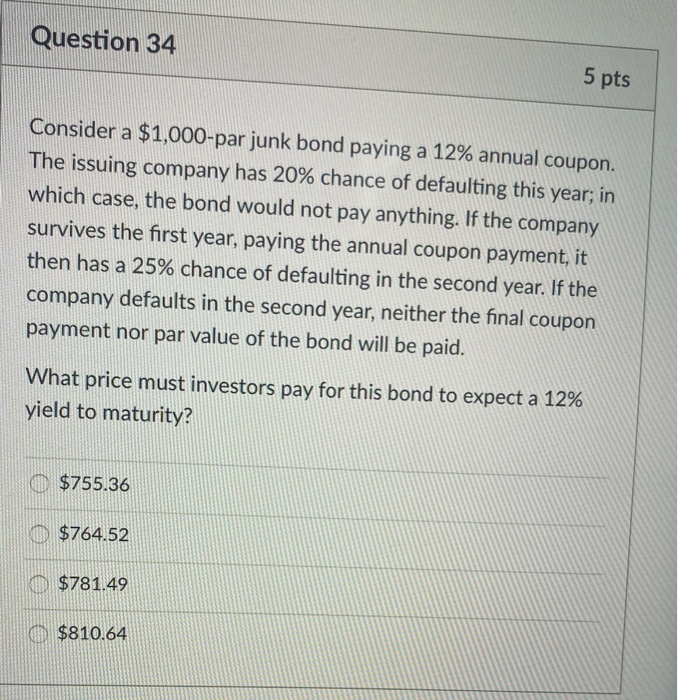
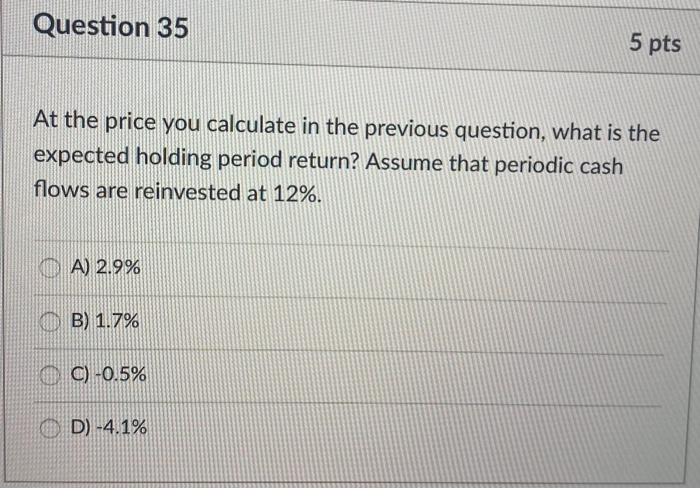
Question 34 5 pts Consider a $1,000-par junk bond paying a 12% annual coupon. The issuing company has 20% chance of defaulting this year; in which case, the bond would not pay anything. If the company survives the first year, paying the annual coupon payment, it then has a 25% chance of defaulting in the second year. If the company defaults in the second year, neither the final coupon payment nor par value of the bond will be paid. What price must investors pay for this bond to expect a 12% yield to maturity? $755.36 0 $764.52 $781.49 $810.64 Par Value = 1000 | Annual Coupon rate = 12% | Annual coupon = 12% * 1000 = 120 Year 1: Chance of Default = 20% Chance of Payment = 80% Expected cashflow = Chance of Default * 0 + Chance of Payment * Coupon Expected cashflow in Year 1 = 20% * 0 + 80%* 120 = 96 Year 2: Chance of Default = 25% Chance of Payment = 75% Expected cashflow = Chance of Default * 0 + Chance of Payment * (Coupon + Principal) Expected cashflow in Year 2 = 25% * 0 + 75%* (120 + 1000) = 840 Price of Bond at 12% YTM = PV of Year 1 Expected Cashflow + PV of Year 2 Expected Cashflow Price of Bond at 12% YTM = 96 / (1+12%) + 840 / (1+12%)2 Price of Bond at 12% YTM = 85.71 + 669.64 = $ 755.36 Hence, Investors mus pay $ 755.36 for the bond to expect a 12% YTM, which is the 1st Option. Question 35 5 pts At the price you calculate in the previous question, what is the expected holding period return? Assume that periodic cash flows are reinvested at 12%. TO A) 2.9% KUD B) 1.7% EC) -0.5% OD -4.1%