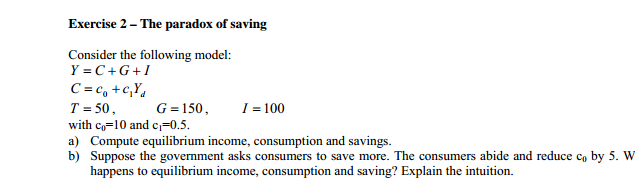
Answers please

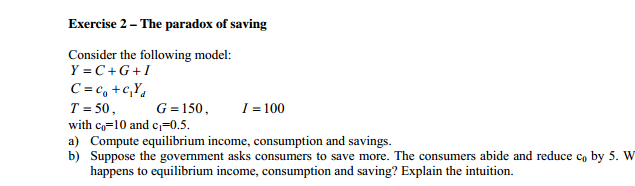
Exercise 5 An expected-utility-maximizing decision maker professes to have constant ab- solute risk aversion over the range of (euro) prizes from s\Exercise 1 - Calculating GDP In an economic system there are two sectors, A and B. The sector A: - produces value added for a value of 50; pays wages for a value of 30; sells intermediate goods to sector B for a value of 15. In the same year, sector B: purchases intermediate goods from sector A for 15 and from abroad for a value of 10: pays wages for a value of 20; 1 sells final goods for a value of 40, of which 10 goes abroad; sells investment goods for a value of 10, of which 5 goes abroad. Compute the GDP of this economic system, by describing and explaining the possible definitions that can be employed.Exercise 2 - The paradox of saving Consider the following model: Y =C+G+I C= co+GYd T = 50, G =150, / = 100 with co=10 and c1=0.5. a) Compute equilibrium income, consumption and savings. b) Suppose the government asks consumers to save more. The consumers abide and reduce co by 5. W happens to equilibrium income, consumption and saving? Explain the intuition.Exercise 3 - The money market In country A the quantity of money (M) in the year 2000 was equal to 450 billion euro. In the same year the ratio of money held in currency (c) and the ratio of reserves/deposits (0) took on the following values: c = 0.2 and 9=0.4. a) Compute the supply of central bank money in 2000. b) What is the money multiplier? c) Suppose the central bank can perfectly control the value of the ratio reserves/deposits (0). If in 2001 the central bank wanted to increase the money supply to 675 billion euro, by how much must Ovary if H and c remain constant at their 2000 levels?Exercise 4 - Fiscal Policy Consider the following numerical version of IS-LM model: C = 400 + 0.5Y I = 700 - 4,0001 + 0.IY G = 200 T = 200 M /P = 0.5Y - 7,5001 M /P = 500 a) Calculate the equilibrium level of income and interest rate. b) Suppose the government increases public spending to 300 (AG =100). Compute the new equilibrium values of income and interest rate. c) Suppose the government decreases taxes to 100 (AT = -100). Compute the new equilibrium values of income and interest rate. d) Compare the results you have found in (b) and (c). Provide an economic explanation for the variation. If the government wants to finance the change in G by increasing T same amount (AT = 100), what happens to the economy