Any help is greatly appreciated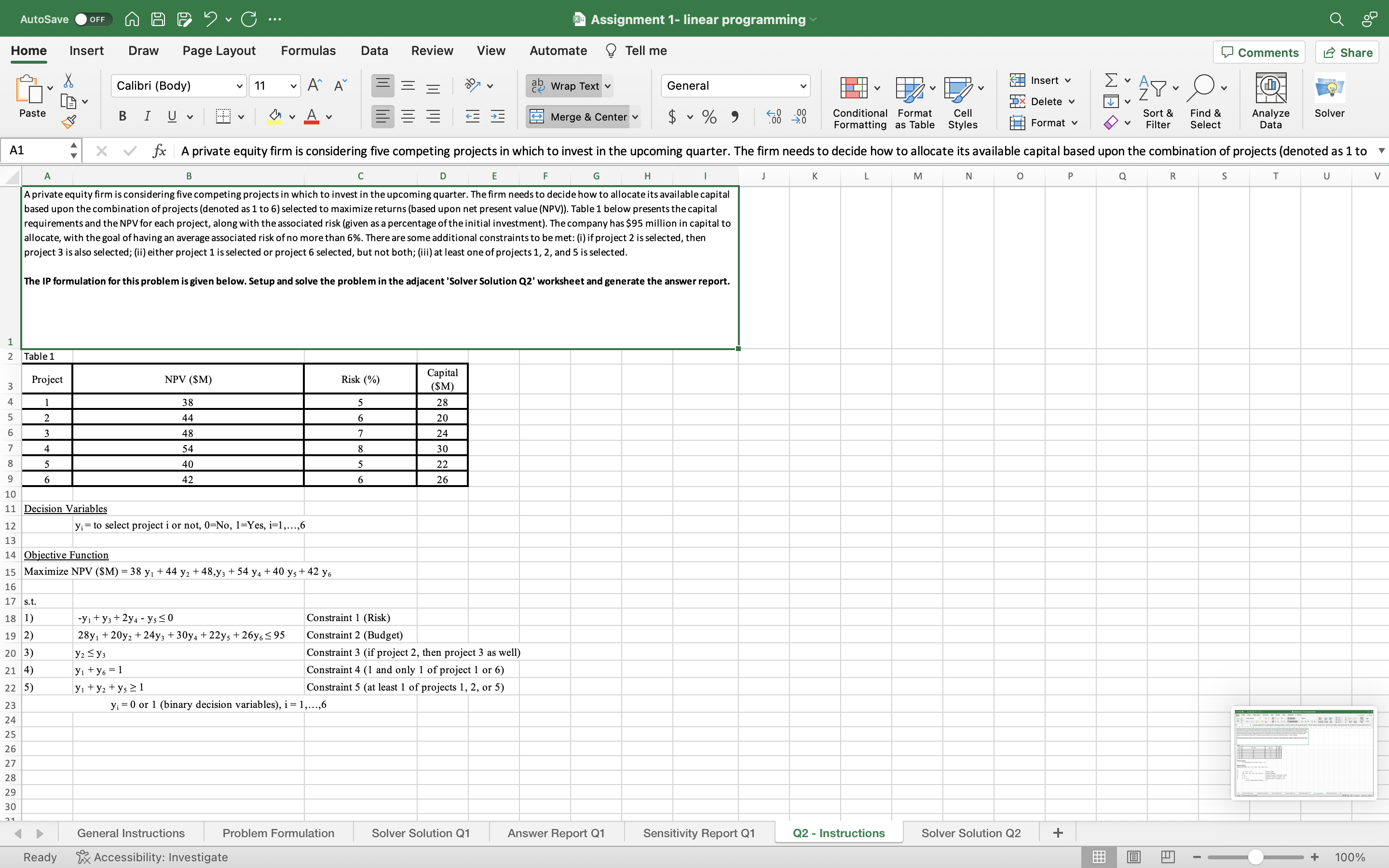

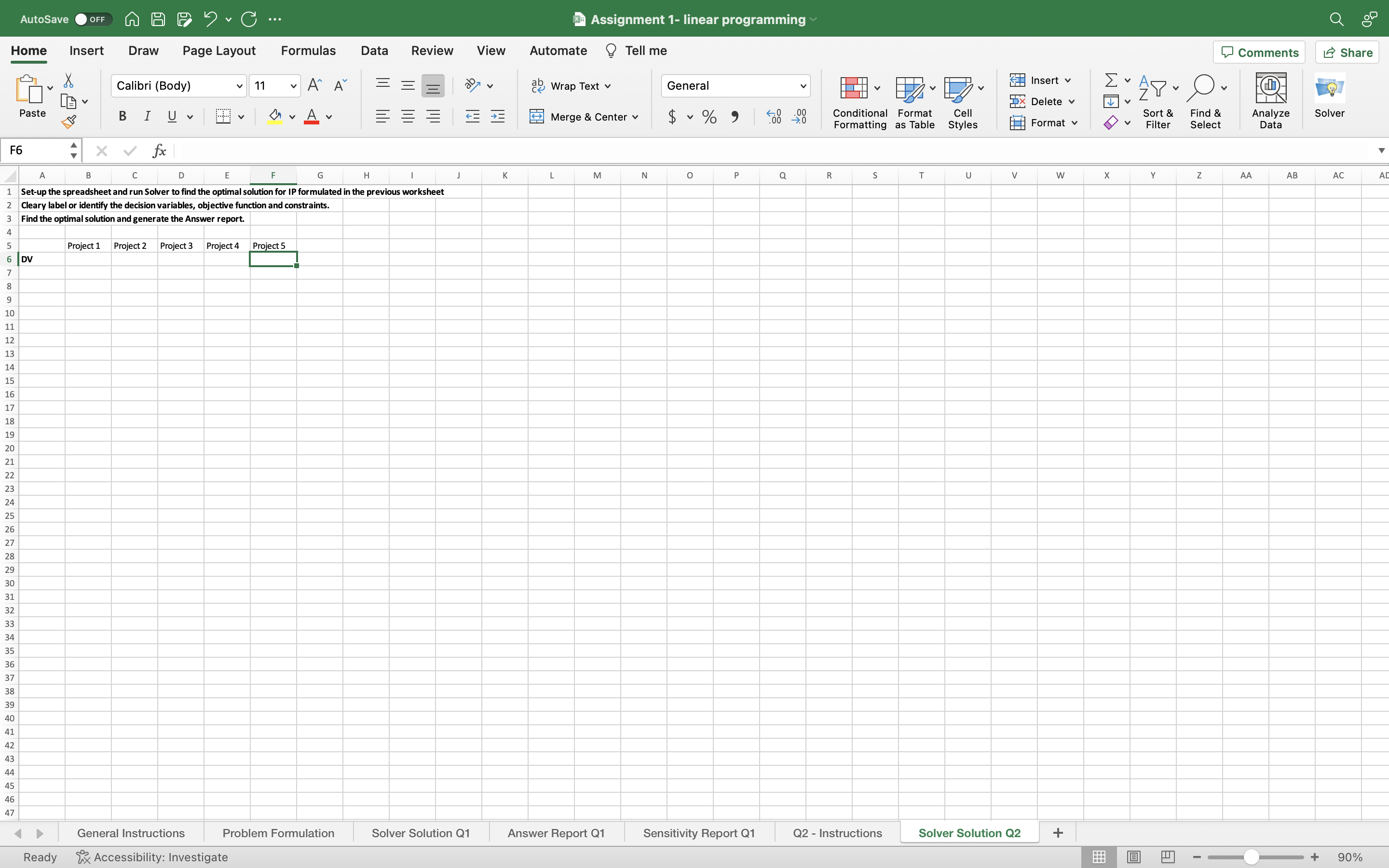
AutoSave Assignment 1- linear programming Home Insert Draw Page Layout Formulas Data Review View Automate A1 A C Duarter. The firm needs to decide how to allocate its available capital based upon the combination of projects (denoted as 1 to 6 ) selected to maximize returns (based upon net present value (NPV)). Table 1 below presents the capital requirements and the NPV for each project, along with the associated risk (given as a percentage of the initial investment). The company has $95 million in capital to allocate, with the goal of having an average associated risk of no more than 6%. There are some additional constraints to be met: (i) if project 2 is selected, then project 3 is also selected; (ii) either project 1 is selected or project 6 selected, but not both; (iii) at least one of projects 1,2 , and 5 is selected. The IP formulation for this problem is given below. Setup and solve the problem in the adjacent 'Solver Solution Q2' worksheet and generate the answer report. Table 1 \begin{tabular}{|c|c|c|c|} \hline Project & NPV ($M) & Risk (\%) & Capital($M) \\ \hline 1 & 38 & 5 & 28 \\ \hline 2 & 44 & 6 & 20 \\ \hline 3 & 48 & 7 & 24 \\ \hline 4 & 54 & 8 & 30 \\ \hline 5 & 40 & 5 & 22 \\ \hline 6 & 42 & 6 & 26 \\ \hline \end{tabular} Decision Variables yi=toselectprojectiornot,0=No,1=Yes,i=1,,6 Objective Function Maximize NPV ($M)=38y1+44y2+48,y3+54y4+40y5+42y6 s.t. (1) 9 (2) y1+y3+2y4y50 28y1+20y2+24y3+30y4 Constraint 1 (Risk) 3) y2y3 Constraint 2 (Budget) 4) y1+y6=1 Constraint 3 (if project 2 , then project 3 as well) 5) y1+y2+y51 Constraint 4 (1 and only 1 of project 1 or 6 ) yi=0 or 1 (binary decision variables), i=1,,6 53 25 26 28 30 Ready Rx Accessibility: Investigate 1+100% AutoSave Assignment 1- linear programming Home Insert Draw Page Layout Formulas Data Review View Automate _Tell me F6 fx 2 Cleary label or identify the decision variables, objective function and constraints. Find the optiabel identify the decision variables, objective function and constraints. 3 Find the optimal solution and generate the Answer report. 4 5 5 6 7 \begin{tabular}{|l|l|l|l|l|} \hline Project 1 & Project 2 & Project 3 & Project 4 & Project 5 \\ \hline & & & & \\ \hline \end{tabular} DV Ready General Instructions Solver Solution Q1 Answer Report Q1 Sensitivity Report Q1 Q2 - Instructions Solver Solution Q2 W AutoSave Assignment 1- linear programming Home Insert Draw Page Layout Formulas Data Review View Automate A1 A C Duarter. The firm needs to decide how to allocate its available capital based upon the combination of projects (denoted as 1 to 6 ) selected to maximize returns (based upon net present value (NPV)). Table 1 below presents the capital requirements and the NPV for each project, along with the associated risk (given as a percentage of the initial investment). The company has $95 million in capital to allocate, with the goal of having an average associated risk of no more than 6%. There are some additional constraints to be met: (i) if project 2 is selected, then project 3 is also selected; (ii) either project 1 is selected or project 6 selected, but not both; (iii) at least one of projects 1,2 , and 5 is selected. The IP formulation for this problem is given below. Setup and solve the problem in the adjacent 'Solver Solution Q2' worksheet and generate the answer report. Table 1 \begin{tabular}{|c|c|c|c|} \hline Project & NPV ($M) & Risk (\%) & Capital($M) \\ \hline 1 & 38 & 5 & 28 \\ \hline 2 & 44 & 6 & 20 \\ \hline 3 & 48 & 7 & 24 \\ \hline 4 & 54 & 8 & 30 \\ \hline 5 & 40 & 5 & 22 \\ \hline 6 & 42 & 6 & 26 \\ \hline \end{tabular} Decision Variables yi=toselectprojectiornot,0=No,1=Yes,i=1,,6 Objective Function Maximize NPV ($M)=38y1+44y2+48,y3+54y4+40y5+42y6 s.t. (1) 9 (2) y1+y3+2y4y50 28y1+20y2+24y3+30y4 Constraint 1 (Risk) 3) y2y3 Constraint 2 (Budget) 4) y1+y6=1 Constraint 3 (if project 2 , then project 3 as well) 5) y1+y2+y51 Constraint 4 (1 and only 1 of project 1 or 6 ) yi=0 or 1 (binary decision variables), i=1,,6 53 25 26 28 30 Ready Rx Accessibility: Investigate 1+100% AutoSave Assignment 1- linear programming Home Insert Draw Page Layout Formulas Data Review View Automate _Tell me F6 fx 2 Cleary label or identify the decision variables, objective function and constraints. Find the optiabel identify the decision variables, objective function and constraints. 3 Find the optimal solution and generate the Answer report. 4 5 5 6 7 \begin{tabular}{|l|l|l|l|l|} \hline Project 1 & Project 2 & Project 3 & Project 4 & Project 5 \\ \hline & & & & \\ \hline \end{tabular} DV Ready General Instructions Solver Solution Q1 Answer Report Q1 Sensitivity Report Q1 Q2 - Instructions Solver Solution Q2 W