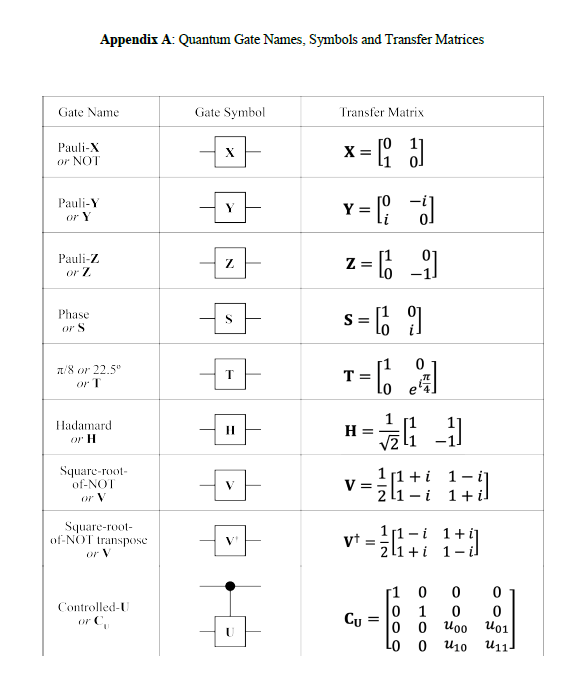
Appendix A: Quantum Gate Names, Symbols and Transfer Matrices Gate Name Gate Symbol Transfer Matrix Pauli-X X or NOT x = Q al Pauli-Y Y or Y Y = [ ] Pauli-Z or 7. Phase S or S s = [ 9 7/8 or 22.5" T OF T T= | Hadamard or H Square-root- of-NOT V V =: 1 1+i 1-1 or V Square-root- of-NOT transpose i 1+i or V vt = zhi+i 0 0 0 Controlled-U Cu = 10 1 0 0 or L 0 101 0 U10 U112. {15 points) Given a qubit with an initial state of |'-F) 2 ll}. yourjob is to cause the qubit to evolve to a position on the Bloch sphere that is lying exactly on the positive yaxis. Your answer should be in the form of a neatly drawn quantum circuit. You may use any of the gates in the table provided in Appendix A (appended to the last page of this test) and you may use as many of them as you would like. However. for full credit. your circuit should contain as few gates as possible. For controlled U gates. you may only use {Cm C\" C1; C5, C1, CH.CV,CV1] . that is. Appendix A gives the general form for a controlledU gate and you may only use U E [3. In I. S; T; H. V; W} in your answer to this problem. You may n_ot introduce any ancilla-"garbage qubits into your solution