Appendix is below for more information.

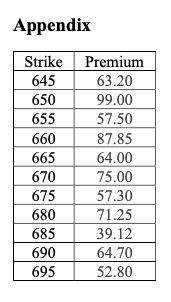
1. The appendix at the end contains the prices of a set of Google Call options. They have 59 days to maturity (T=59 days). Suppose the risk-free rate is 0% per annum. The stock price of Google was 738.06. Assume all the options are European Options. a. Find two options for which the low boundary condition DOES NOT Hold and thus arbitrage opportunities exist. Calculate the minimum arbitrage profit. Option 1: Strike 645 _; Profit per Contract 29.86 Option 2: Strike 655 _; Profit per Contract 25.56 In general, if a call option does not satisfy the low boundary condition, we sell (buy/sell) the option, long (long/short) the stock, and lend (lend/Borrow) to realize arbitrage profit. b. Find two pairs of options for which the relationship C(K) > C(K2) for KZ > K DOES NOT HOLD and thus arbitrage opportunities exist. Calculate the minimum arbitrage profit. Pair 1: Strikes 645 and 650 ; Minimum Profit_45.80 Pair 2: Strikes 655 and 660 ; Minimum Profit 30.35 In general, if the relationship does not hold, we (buy/sell) the option with high strike price, (buy/sell) the option with low strike price. c. Find two pairs of options for which the relationship C(K)-C(K) = K2 - Ki for K2 > K DOES NOT HOLD and thus arbitrage opportunities exist. Calculate the minimum arbitrage profit. Pair 1: Strikes and ; Minimum Profit Pair 2: Strikes _and ; Minimum Profit In general, if the relationship does not hold, we_ _(buy/sell) the option with high strike price, (buy/sell) the option with low strike price. d. Find three triples of options for which, one can construct a risk-free long butterfly strategy and calculate the maximum and minimum profit. Triple 1: Strikes __ , and . Maximum profit __and minimum profit_ Triple 2: Strikes __ _. Maximum profit and minimum profit Triple 3: Strikes . Maximum profit and minimum profit and wand Appendix Strike 645 650 655 660 665 670 675 Premium 63.20 99.00 57.50 87.85 64.00 75.00 57.30 71.25 39.12 64.70 52.80 680 685 690 695 1. The appendix at the end contains the prices of a set of Google Call options. They have 59 days to maturity (T=59 days). Suppose the risk-free rate is 0% per annum. The stock price of Google was 738.06. Assume all the options are European Options. a. Find two options for which the low boundary condition DOES NOT Hold and thus arbitrage opportunities exist. Calculate the minimum arbitrage profit. Option 1: Strike 645 _; Profit per Contract 29.86 Option 2: Strike 655 _; Profit per Contract 25.56 In general, if a call option does not satisfy the low boundary condition, we sell (buy/sell) the option, long (long/short) the stock, and lend (lend/Borrow) to realize arbitrage profit. b. Find two pairs of options for which the relationship C(K) > C(K2) for KZ > K DOES NOT HOLD and thus arbitrage opportunities exist. Calculate the minimum arbitrage profit. Pair 1: Strikes 645 and 650 ; Minimum Profit_45.80 Pair 2: Strikes 655 and 660 ; Minimum Profit 30.35 In general, if the relationship does not hold, we (buy/sell) the option with high strike price, (buy/sell) the option with low strike price. c. Find two pairs of options for which the relationship C(K)-C(K) = K2 - Ki for K2 > K DOES NOT HOLD and thus arbitrage opportunities exist. Calculate the minimum arbitrage profit. Pair 1: Strikes and ; Minimum Profit Pair 2: Strikes _and ; Minimum Profit In general, if the relationship does not hold, we_ _(buy/sell) the option with high strike price, (buy/sell) the option with low strike price. d. Find three triples of options for which, one can construct a risk-free long butterfly strategy and calculate the maximum and minimum profit. Triple 1: Strikes __ , and . Maximum profit __and minimum profit_ Triple 2: Strikes __ _. Maximum profit and minimum profit Triple 3: Strikes . Maximum profit and minimum profit and wand Appendix Strike 645 650 655 660 665 670 675 Premium 63.20 99.00 57.50 87.85 64.00 75.00 57.30 71.25 39.12 64.70 52.80 680 685 690 695