APPLICATION $1($Optimization$)$:

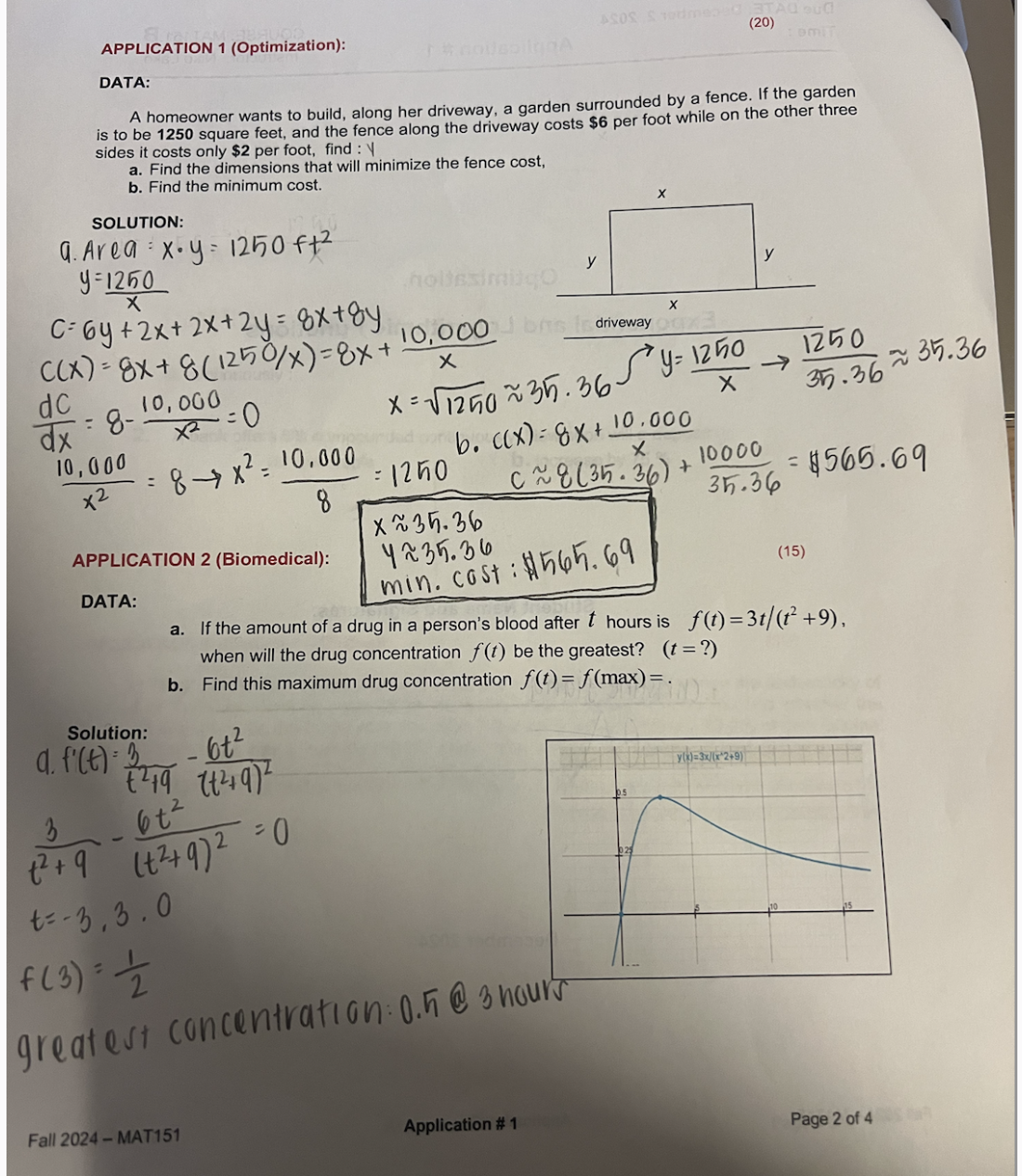
DATA:

A homeowner wants to build, along her driveway, a garden surrounded by a fence. If the garden

is to be $1250$ square feet, and the fence along the driveway costs $$6$ per foot while on the other three

sides it costs only $$2$ per foot, find : Y

a$.$ Find the dimensions that will minimize the fence cost

b$.$ Find the minimum cost.

SOLUTION:

a$.$ Area : x$*$y$=1250$ft$^(2)$

y$=(1250)/($x$)$

C$=6$y$+2$x$+2$x$+2$y$=8$x$+8$y

c$($x$)=8$x$+8((1250)/($x$))=8$x$+(10,000)/($x$)$

$($dc$)/($dx$)=8-(10\mathrm{.}000)/($x$^(2))=0,$x$=\backslash$sqrt$(1250)$~~$35\mathrm{.}36\backslash$int $(1250)/($x$)->(1250)/(35\mathrm{.}36)$~~$35\mathrm{.}36$

$\{($:$[(10,000)/($x$^(2))=8->$x$^(2)=(10\mathrm{.}000)/(8$ b$.$ c$($x$))=8$x$+(10\mathrm{.}000)/($x$)=1250,$c~~$8(35\mathrm{.}36)+(10000)/(35\mathrm{.}36)=$$$565\mathrm{.}69)$:$\}$

x~~$35\mathrm{.}36]$

APPLICATION $2($Biomedical$)$:

x~~$35\mathrm{.}36$

y~~$35\mathrm{.}36$

min. cost : $$565\mathrm{.}69$

DATA:

a$.$ If the amount of a drug in a person's blood after t hours is f$($t$)=3($t$)/($t$^(2)+9),$

when will the drug concentration f$($t$)$ be the greatest? $?$f$($t$)=$f$($max$)=.$

Solution:

a$.$ f$^(\text{'})($t$)=(3$t$^(2))/($t$^(2)+9)-(6$t$^(2))/(($t$^(2)+9)^(2))$

$(3)/($t$^(2)+9)-(6$t$^(2))/(($t$^(2)+9)^(2))=0$

t$=-3,3*0$

f$(3)=(1)/(2)$

greatest concentration: $0\mathrm{.}5$ e s no