Question: Application - Differentials: Problem 1 (1 point) The figure shows how a function f() and its linear approximation (i.e., its tangent line) change value when

value when I changes from To to y = f(x) To +

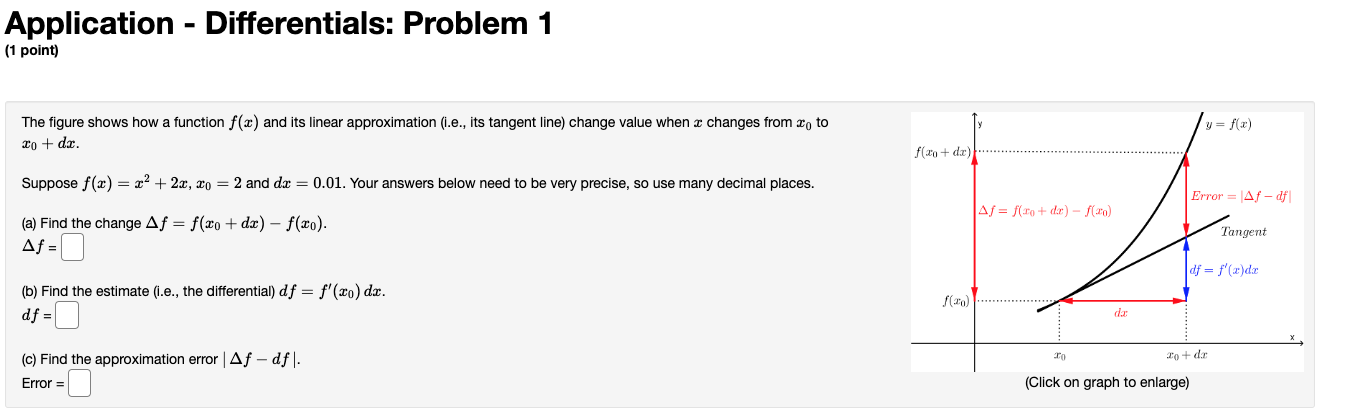
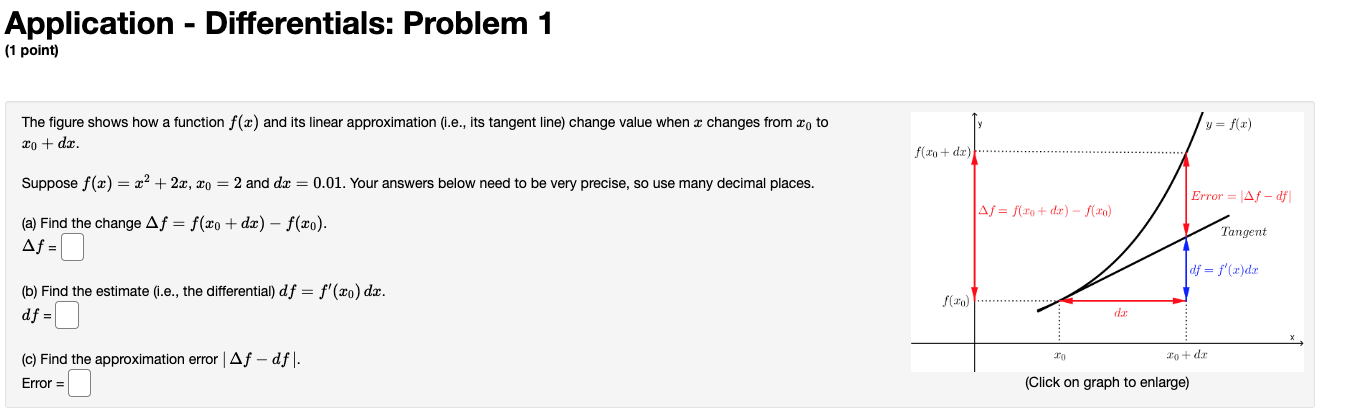
dr. f(xo + dr)......... Suppose f(x) = x2 + 2x, x0 =

2 and dar = 0.01. Your answers below need to be very

Application - Differentials: Problem 1 (1 point) The figure shows how a function f() and its linear approximation (i.e., its tangent line) change value when I changes from To to y = f(x) To + dr. f(xo + dr)......... Suppose f(x) = x2 + 2x, x0 = 2 and dar = 0.01. Your answers below need to be very precise, so use many decimal places. Error = 14f - dfl (a) Find the change Af = f(xo + dx) - f(x0). Af = f(ro+ de) - f(zo) Tangent Af = df = f(x)de (b) Find the estimate (i.e., the differential) df = f'(xo) dx. f(zo) df = da (c) Find the approximation error | Af - dif |. To + da Error = (Click on graph to enlarge)Application - Differentials: Problem 2 (1 point) Suppose that f() is a function with f(120) = 28 and f'(120) = 1. Estimate f(124.5). f (124.5) =Application - Differentials: Problem 3 {1 point} Let y = {in2 + 5)'. Find the differential dy when a: = 5 and do: = 0.3 Find the differential dy when a: = 5 and do: = 0.01

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Need help (1 point) The figure shows how a function f(z) and its linear approximation (i.e, its tangent line) change value when I changes from co to co + dr. Suppose f(x) = 12 - 61, TO = 3 and dx =...

(10 points) y = f(2) The figure shows how a function f() and its linear approximation (i.e., its tangent line) change value when a changes from To to To + de. Suppose f(x) = x2 - 5x, To = 2 and da =...

co 1.8 The Tangent Line Approxim X + edfinity.com/assessments/64a2f4b1512d2700256163a0?start=t Fue Press (fn) F to exit full screen GR AIR edfinity 1.8 The Tangent Line Approximation OPEN Turned in...

Calculus Questions (4.1 & 4.2) 1. dy Find at = = 1ify= = +4 and = 1 dt dt dtdr dA Let A be the area of a circle with radius r. If = 5, find dt when r = 4. dtA spherical snowball is melting in such a...

please answer/correct these problems: Section 2.8: Problem 1 (1 point) Previous Problem Problem List Next Problem The linear approximation at * = 0 to f(@ ) = is 8 L(x) = A+ Bx where A = B =Problem...

Use linear approximation, i.e. the tangent line, to approximate V251 as follows: Let HI] = 1,5.Find the equation of the tangent line to st) at I = 2-5 new: Using this, we find our approximation for v...

Home > Math 261 Calc- | Summer 2023 >Assessment 2.8 Progresssaved Done lg 15' Score: 039 D-"9 answered 0 Question1 v 8 m1 pt '0 5 2:3 2 G) Details Use linear approximation, i.e. the tangent line, to...

Identify the tax issue or issues suggested by the following situations and state each issue in the form of a question. This year, Ms. T had a $29,000 capital loss carry forward and a $8,200 suspended...

Olivia has received a $15 gift certificate that is redeemable only for roasted peanuts. Bags of roasted peanuts come in two sizes, regular and jumbo. A regular bag contains 30 peanuts and a jumbo bag...

Why is employment a macroeconomic objective of all governments?

9 (A) Cognitive institution constitutes of codified sets of laws and regulations and government policies. (B) The threats of new entrants are low when the industry has high degree of expected...

3. List four points that you think are important to give the individual attention, when he or she is going to sell an argument or an idea to you.

4. Think of a situation where you would convince someone of an argument or an idea you had. a. What feelings did you want the other person to be left with when you finished? b. When you think about...

7. Think of a situation where you felt that you mastered the situation, i.e. where you had a positive feeling of completing the task you were to perform. A. Now develop a picture in your imaginary...