Application Example for FTA Calculation Methods

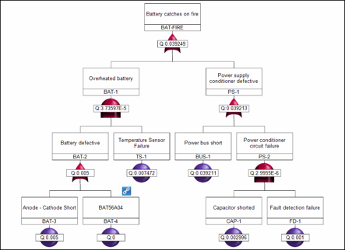
The following time dependent fault tree is used to demonstrate how the FTA module supports the cut$-$set based and exact calculation methods. The FTA module also supports simulation, which uses varying sets of inputs to observe the dynamic behavior of the tree.

$($ View image $1)$

The top event for this static tree, Motor Overheats, has three minimal cut sets: C$1=$ Event A; C$2=$ Event B and Event C; and C$3=$ Event B and Event D$.$ The top event occurs if at least one of these cut sets occurs. For simplicity, Event X is referred to as X and the probability of Event X is referred to as Pr$\{$X$\}.$ The event probabilities used are: Pr$\{$A$\}=0\mathrm{.}1$; Pr$\{$B$\}=0\mathrm{.}2$; Pr$\{$C$\}=0\mathrm{.}25$; and Pr$\{$D$\}=0\mathrm{.}3.$

While the FTA module supports several calculation results for time dependent trees, including unavailability, unreliability, importance measures, frequency, and number of failures, this example concentrates on unavailability calculations.

Cut Set Summation

The cut set summation method is based on the assumption that the probability of the simultaneous occurrence of multiple cut sets is negligible. Hence, cut sets can be considered as mutually exclusive events. This is applicable only if individual cut set probabilities are very low. Always producing conservative results for coherent trees, this method first calculates the probability of each cut set, which is the product of the probabilities of all events in that cut set. Thus, for the top event in the example, Pr$\{$C$1\}=0\mathrm{.}1,$ Pr$\{$C$2\}=0\mathrm{.}05,$ and Pr$\{$C$3\}=0\mathrm{.}06.$ The top event probability is the sum of the probabilities of all cut sets or $0\mathrm{.}1+0\mathrm{.}05+0\mathrm{.}06=0\mathrm{.}21.$

Cross Product

The cross$-$product method uses Poincare$$s inclusion$-$exclusion formula. The number of order of terms in the expansion is equal to the number of cut sets. First order terms include the individual cut sets; second order terms include all combinations of two cut sets; and so on$.$ The sign for each order of terms changes alternately. For this example:

$($view image$2)$

The intersection of cut sets includes all events present in the cut sets, but only once. When all three order of terms are considered: Pr$\{$TOP$\}=0\mathrm{.}1855,$ which is the exact result. Because higher order terms generally contain more events, whose combined occurrence is negligible, they can be eliminated to reduce computational time. If only first order terms are considered, the result matches that from the cut set summation method: Pr$\{$TOP$\}=0\mathrm{.}21.$ If second order terms are considered: Pr$\{$TOP$\}=0\mathrm{.}184.$

Esary Proschan

The Esary Proschan method considers all cut sets to be independent, which is an acceptable approximation for most cases. For coherent trees, this approximation always leads to conservative results. This method first calculates the probabilities of individual cut sets. Assuming cut sets are independent, the top event probability is calculated: Pr$\{$TOP$\}=1(1-0\mathrm{.}1)*(1-0\mathrm{.}05)*(1-0\mathrm{.}06)=0\mathrm{.}1963.$ This value is greater than the exact answer of $0\mathrm{.}1855.$ It is also a better upper bound than the $0\mathrm{.}21$ value provided by the cut set summation method. This method can be improved even further if all cut sets contain some common events.

Exact

To overcome the difficulties associated with cut set$-$based methods and to improve the accuracy and speed of calculations, the FTA module supports various advanced methods to compute exact results. These methods, collectively called the Exact method, utilize the latest research advances in computing fault trees. Based on the tree being analyzed, this method uses an appropriate set of solution techniques. They include modularization, automatic generation of Markov chains for dynamic modules, bottom$-$up method, pivotal decomposition method, and efficient algorithms for calculating frequency and importance measures. Using the Exact method, the unavailability is $0\mathrm{.}1855.$

Conclusion

For this example, the exact unavailability of the top event is $0\mathrm{.}1855.$ Using the Exact method always produces this result. For the cut set$-$based methods, the unavailability result falls between $0\mathrm{.}1963$ and $0\mathrm{.}21.$ This demonstrates how cut set results are approximations, and how you can use calculation properties to control the approximation to ensure results are within the accuracy range that you require.

The advantage of using cut$-$set based methods is that they quickly generate results for large trees while maintaining needed accuracy levels. Because very large trees and those with complex configurations can require lengthy computation times, they are more suited to cut set$-$based methods.

To significantly reduce computational time for cut set$-$based methods even further, you can use the Ignore cut sets with probabilities less than and Ignore cut sets with an order greater than properties to eliminate insignificant cut sets. Both of these properties appear on the FTA $>$ General page in the Calculate window.