Application: Linear Programming Data Fitting

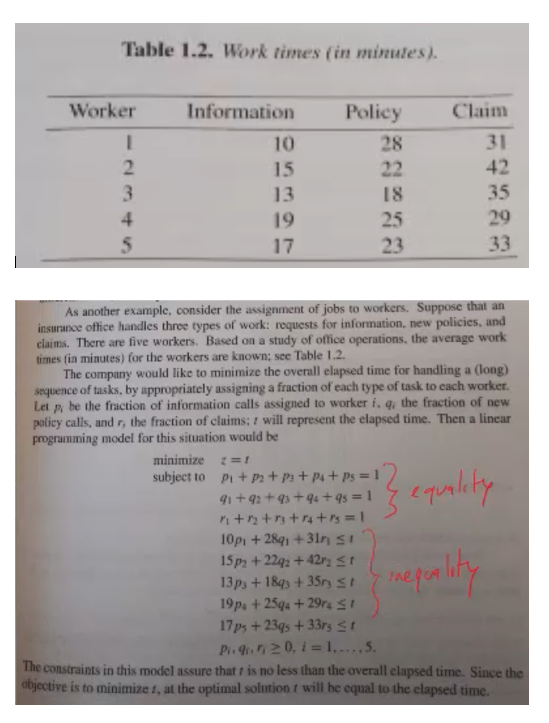
Table 1.2. Work times (in minutes). Worker 1 2 3 4 5 Information 10 15 13 19 17 Policy 28 22 18 25 23 Claim 31 42 35 29 33 As another example, consider the assignment of jobs to workers. Suppose that an insurance office handles three types of work: requests for information, new policies, and claims. There are five workers. Based on a study of office operations, the average work times in minutes) for the workers are known; see Table 1.2. The company would like to minimize the overall elapsed time for handling a (long) sequence of tasks, by appropriately assigning a fraction of each type of task to each worker. Let be the fraction of information calls assigned to worker i. qi the fraction of new policy calls, and r, the fraction of claims: 7 will represent the elapsed time. Then a linear programming model for this situation would be minimize = 1 subject to P+pa+p+ Pu+Ps = 1 41 +92 +93 +94 +95 = 1 1 + 2 + 3 + 4 + 1 = 1 10p. + 2891 +3in si 15p2 +2242 +42r, St 13ps + 1893 +35r3 st 19p. + 2594 + 294 SI 17ps +239 + 33r3 S1 Pi8.20, i = 1, ...,5. The constraints in this model assure that is no less than the overall elapsed time. Since the objective is to minimize , at the optimal solution t will be equal to the clapsed time. } equality inequality Table 1.2. Work times (in minutes). Worker 1 2 3 4 5 Information 10 15 13 19 17 Policy 28 22 18 25 23 Claim 31 42 35 29 33 As another example, consider the assignment of jobs to workers. Suppose that an insurance office handles three types of work: requests for information, new policies, and claims. There are five workers. Based on a study of office operations, the average work times in minutes) for the workers are known; see Table 1.2. The company would like to minimize the overall elapsed time for handling a (long) sequence of tasks, by appropriately assigning a fraction of each type of task to each worker. Let be the fraction of information calls assigned to worker i. qi the fraction of new policy calls, and r, the fraction of claims: 7 will represent the elapsed time. Then a linear programming model for this situation would be minimize = 1 subject to P+pa+p+ Pu+Ps = 1 41 +92 +93 +94 +95 = 1 1 + 2 + 3 + 4 + 1 = 1 10p. + 2891 +3in si 15p2 +2242 +42r, St 13ps + 1893 +35r3 st 19p. + 2594 + 294 SI 17ps +239 + 33r3 S1 Pi8.20, i = 1, ...,5. The constraints in this model assure that is no less than the overall elapsed time. Since the objective is to minimize , at the optimal solution t will be equal to the clapsed time. } equality inequality