Applied Linear Algebra - Nearest Point to a line. I have attached page 18 below the question.

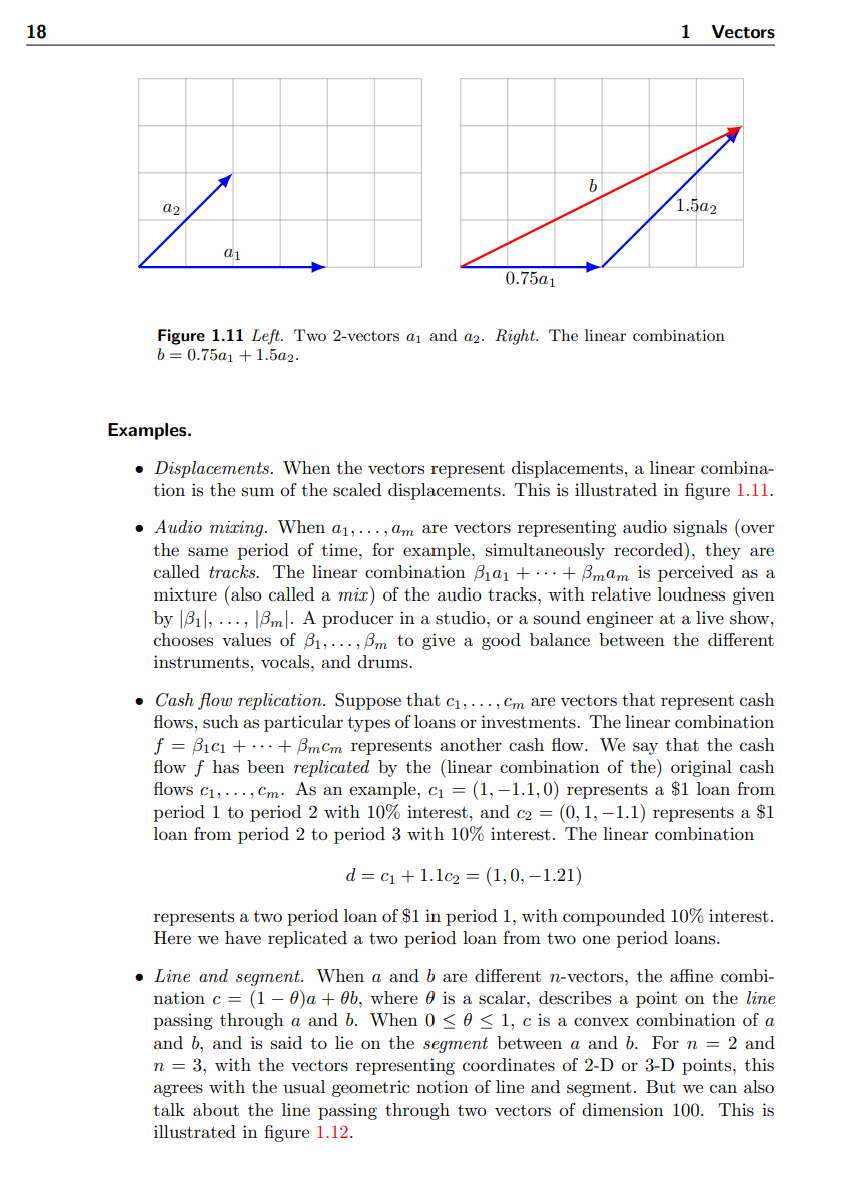
3.12 Nearest point to a line. Let a and b be different art-vectors. The line passing through a and b is given by the set of vectors of the form (1 9)a + 6b, where 6 is a scalar that determines the particular point on the line. (See page 18.) Let .7: be any n-vector. Find a formula for the point p on the line that is closest to m. The point p is called the projection of 5*: onto the line. Show that (p 9:) l (a b), and draw a simple picture illustrating this in 2-D. Hint. Work with the square of the distance between a point on the line and 3:, 116., \"(1 (9)0. + 9b $\"2. Expand this, and minimize Over 6. 18 1 Vectors b a2 1.5a2 a1 0.75a1 Figure 1.11 Left. Two 2-vectors a, and a2. Right. The linear combination b = 0.75a1 + 1.5a2. Examples. . Displacements. When the vectors represent displacements, a linear combina- tion is the sum of the scaled displacements. This is illustrated in figure 1.11. . Audio mixing. When a1, . .., am are vectors representing audio signals (over the same period of time, for example, simultaneously recorded), they are called tracks. The linear combination Bid + .. . + 8mam is perceived as a mixture (also called a mir) of the audio tracks, with relative loudness given by Bil, . .., 18ml. A producer in a studio, or a sound engineer at a live show, chooses values of B1, . .., m to give a good balance between the different instruments, vocals, and drums. . Cash flow replication. Suppose that C1, . .., Cm are vectors that represent cash flows, such as particular types of loans or investments. The linear combination f = Bici+ ... + BmCm represents another cash flow. We say that the cash flow f has been replicated by the (linear combination of the) original cash flows C1, . .., Cm. As an example, c1 = (1, -1.1, 0) represents a $1 loan from period 1 to period 2 with 10% interest, and c2 = (0, 1, -1.1) represents a $1 loan from period 2 to period 3 with 10% interest. The linear combination d = ci + 1.1c2 = (1, 0, -1.21) represents a two period loan of $1 in period 1, with compounded 10% interest. Here we have replicated a two period loan from two one period loans. . Line and segment. When a and b are different n-vectors, the affine combi- nation c = (1 -0)a + 0b, where O is a scalar, describes a point on the line passing through a and b. When 0