APPLIED NUMERICAL METHODS GIVING THIS CODE IN MATLAB DO PROBLEM 1 USING NEWTON'S DIVIDED DIFFERENCES SHOW GRAPH AND CODE IN MATLAB

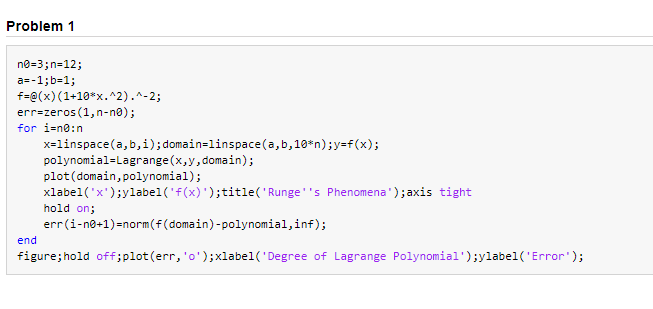
as-1,b=1; f-e(x) (1-10%."2).^-2; err=zeros (1, n-na); for i=n:n x=linspace(a,b,i) ; domain=linspace(a,b,10*n);y-f(x); polynomial-Lagrange(x,y,domain); plot (domain,polynomial); xlabel('x);ylabelf(x) )stitle('Runge 's Phenomena)axis tight hold on err(i-ne+1)-norm(f(domain)-polynomial,inf); end figure;hold off;plot (err, 'o'xlabel('Degree of Lagrange Polynomial');ylabel('Error) as-1,b=1; f-e(x) (1-10%."2).^-2; err=zeros (1, n-na); for i=n:n x=linspace(a,b,i) ; domain=linspace(a,b,10*n);y-f(x); polynomial-Lagrange(x,y,domain); plot (domain,polynomial); xlabel('x);ylabelf(x) )stitle('Runge 's Phenomena)axis tight hold on err(i-ne+1)-norm(f(domain)-polynomial,inf); end figure;hold off;plot (err, 'o'xlabel('Degree of Lagrange Polynomial');ylabel('Error)