Apply matrix theory to linear equations and transformations

Scenario

You are employed as a network engineer and have been asked to analyze a communication network to determine the current data rates and

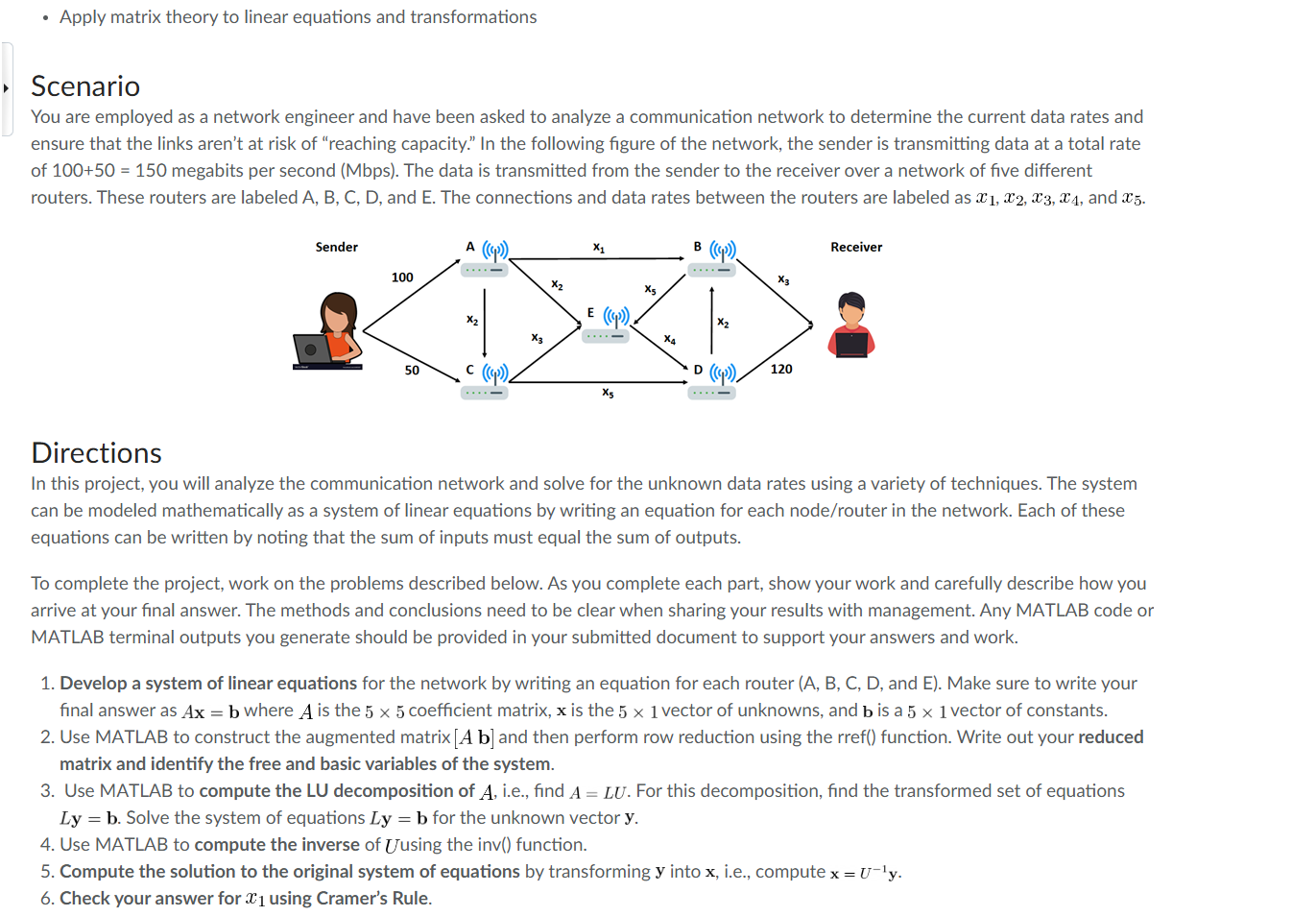
ensure that the links aren't at risk of "reaching capacity." In the following figure of the network, the sender is transmitting data at a total rate

of $100+50=150$ megabits per second $($Mbps$).$ The data is transmitted from the sender to the receiver over a network of five different

routers. These routers are labeled $A,B,C,D,$ and E $.$ The connections and data rates between the routers are labeled as $x_1,x_2,x_3,x_4,$ and $x_5.$

Directions

In this project, you will analyze the communication network and solve for the unknown data rates using a variety of techniques. The system

can be modeled mathematically as a system of linear equations by writing an equation for each node$/$router in the network. Each of these

equations can be written by noting that the sum of inputs must equal the sum of outputs.

To complete the project, work on the problems described below. As you complete each part, show your work and carefully describe how you

arrive at your final answer. The methods and conclusions need to be clear when sharing your results with management. Any MATLAB code or

MATLAB terminal outputs you generate should be provided in your submitted document to support your answers and work.

Develop a system of linear equations for the network by writing an equation for each router $(A,B,C,D,$ and E $).$ Make sure to write your

final answer as $Ax=b$ where $A$ is the $55$ coefficient matrix, $x$ is the $51$ vector of unknowns, and $b$ is a $51$ vector of constants.

Use MATLAB to construct the augmented matrix $Ab$ and then perform row reduction using the rref$()$ function. Write out your reduced

matrix and identify the free and basic variables of the system.

Use MATLAB to compute the LU decomposition of $A,$ i$.$e$.,$ find $A=LU.$ For this decomposition, find the transformed set of equations

$Ly=b.$ Solve the system of equations $Ly=b$ for the unknown vector $y.$

Use MATLAB to compute the inverse of $U$ using the inv$()$ function.

Compute the solution to the original system of equations by transforming $y$ into $x,$ i$.$e$.,$ compute $x=U^{-1}y.$

Check your answer for $x_1$ using Cramer's Rule. Check your answer for $x_1$ using Cramer's Rule.

Use MATLAB to compute the required determinants using the det$()$ function. The Project One Table Template, provided in the Supporting

Materials section, shows the recommended throughput capacity of each link in the network. Put your solution for the system of

equations in the third column so it can be easily compared to the maximum capacity in the second column. In the fourth column of the

table, provide recommendations for how the network should be modified based on your network throughput analysis findings. The

modification options can be No Change, Remove Link, or Upgrade Link. In the final column, explain how you arrived at your

recommendation.

What to Submit

To complete this project, you must submit the following:

Use the provided Project One Template as the starting point for your project solution. Complete each portion of the template, run the

project, and then export your work as a single PDF file. Upload this PDF document, which should show your answers and supporting work

for the problems described above. Make sure to include explanations of your work, as well as all MATLAB code and outputs of the

computations.