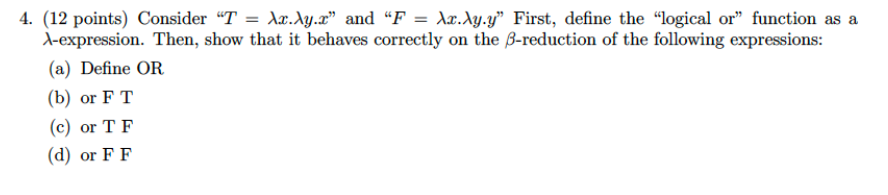
As a reminder, here is the grammar for lambda calculus expressions: Ex^x.E|EE|(E) The rules for parsing with this ambiguous) grammar are: Application is left associative, so "E_E2E2 is parsed as "(E1 E2)E3" Abstraction (2) extends as far right as possible, so "\x.EjE2" is parsed as Xx.(E1 E2)" E= (E) is the grouping rule, so (Ax.E1 E2) Ez is parsed as (Ax.(E1E2))(E3) 4. (12 points) Consider T = dx.dy.x and F = dx.dy.y First, define the logical or function as a -expression. Then, show that it behaves correctly on the B-reduction of the following expressions: (a) Define OR (b) or FT (c) or TF (d) or FF As a reminder, here is the grammar for lambda calculus expressions: Ex^x.E|EE|(E) The rules for parsing with this ambiguous) grammar are: Application is left associative, so "E_E2E2 is parsed as "(E1 E2)E3" Abstraction (2) extends as far right as possible, so "\x.EjE2" is parsed as Xx.(E1 E2)" E= (E) is the grouping rule, so (Ax.E1 E2) Ez is parsed as (Ax.(E1E2))(E3) 4. (12 points) Consider T = dx.dy.x and F = dx.dy.y First, define the logical or function as a -expression. Then, show that it behaves correctly on the B-reduction of the following expressions: (a) Define OR (b) or FT (c) or TF (d) or FF