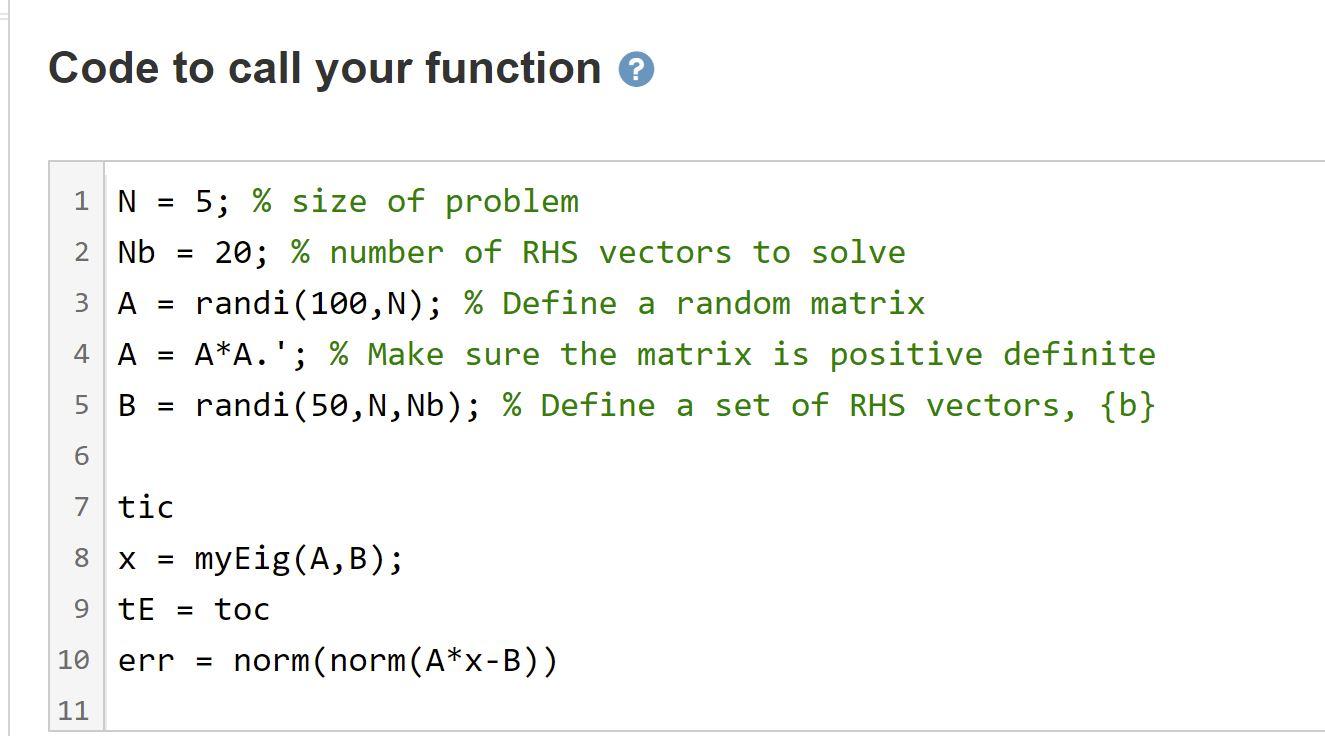
As discussed in class, we can expedite a linear system solution using the eigensolution. This problem demonstrates the effectiveness of this method. The system we are solving is of the form, [A]{x} = {b}, where [A] is assumed to be positive definite. However we want to solve this equation for a series of N, consecutive "steps" in {b}, which we represent as [B] = [{b},{by},..., {bn,}]. A straightforward Gauss-Jordan code with pivoting has been written to solve this system one {b}at a time. Your job is to solve the problem at least 10 times faster under the conditions described below. Your function must be called, function [x] = myEig(A,B) where [A] is a positive definite matrix of size N *N, [B] is N x Nb, and [x] is also N No. Your code will be checked on a system where N = 100, No = 256.[A] will be populated by random integers between 0 and 100, and [B] is populated with random integers between 0 and 50. The competition between the two methods will be run 10 times, and the solution time ratio r = tGauss/teig will be averaged across these 10 iterations. Your error is also checked, but it's the max, not the average error of the 10 runs which must meet the tolerance. Thus if you're pretty sure you have the right answer and you've failed the test, you may try submitting again and you may end up succeeding. Note: Running the pretest provide a quick check on the accuracy of your solution for a single {b} (N = 1). The full check takes longer to run. Code to call your function 2 1 N = 5; % size of problem 2 Nb = 20; % number of RHS vectors to solve 3 A randi(100,N); % Define a random matrix 4 A A*A.'; % Make sure the matrix is positive definite 5 B randi(50,N,Nb); % Define a set of RHS vectors, {b} = 6 7 tic 8 X = 9 tE myEig(A,B); toc = norm(norm(A*x-B)) 10 err 11 As discussed in class, we can expedite a linear system solution using the eigensolution. This problem demonstrates the effectiveness of this method. The system we are solving is of the form, [A]{x} = {b}, where [A] is assumed to be positive definite. However we want to solve this equation for a series of N, consecutive "steps" in {b}, which we represent as [B] = [{b},{by},..., {bn,}]. A straightforward Gauss-Jordan code with pivoting has been written to solve this system one {b}at a time. Your job is to solve the problem at least 10 times faster under the conditions described below. Your function must be called, function [x] = myEig(A,B) where [A] is a positive definite matrix of size N *N, [B] is N x Nb, and [x] is also N No. Your code will be checked on a system where N = 100, No = 256.[A] will be populated by random integers between 0 and 100, and [B] is populated with random integers between 0 and 50. The competition between the two methods will be run 10 times, and the solution time ratio r = tGauss/teig will be averaged across these 10 iterations. Your error is also checked, but it's the max, not the average error of the 10 runs which must meet the tolerance. Thus if you're pretty sure you have the right answer and you've failed the test, you may try submitting again and you may end up succeeding. Note: Running the pretest provide a quick check on the accuracy of your solution for a single {b} (N = 1). The full check takes longer to run. Code to call your function 2 1 N = 5; % size of problem 2 Nb = 20; % number of RHS vectors to solve 3 A randi(100,N); % Define a random matrix 4 A A*A.'; % Make sure the matrix is positive definite 5 B randi(50,N,Nb); % Define a set of RHS vectors, {b} = 6 7 tic 8 X = 9 tE myEig(A,B); toc = norm(norm(A*x-B)) 10 err 11