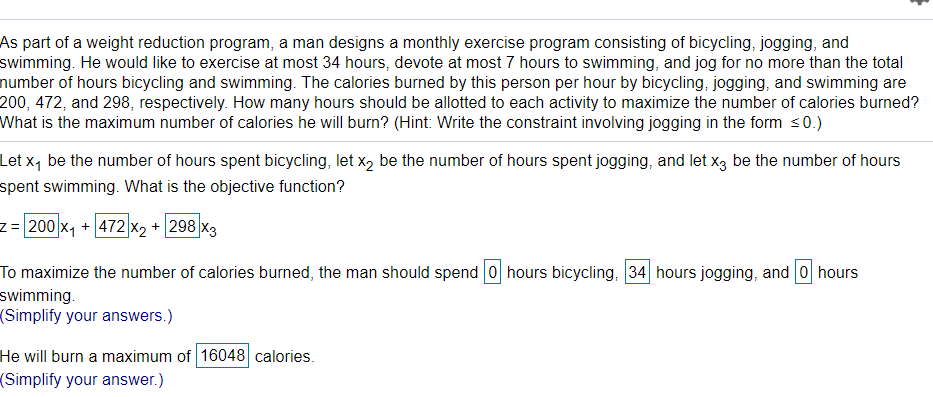
As part of a weight reduction program, a man designs a monthly exercise program consisting of bicycling, jogging, and swimming. He would like to exercise at most 34 hours, devote at most 7 hours to swimming, and jog for no more than the total number of hours bicycling and swimming. The calories burned by this person per hour by bicycling, jogging, and swimming are 200, 472, and 298, respectively. How many hours should be allotted to each activity to maximize the number of calories burned? What is the maximum number of calories he will burn? (Hint: Write the constraint involving jogging in the form s0.) Let xq be the number of hours spent bicycling, let xz be the number of hours spent jogging, and let xz be the number of hours spent swimming. What is the objective function? z= 200 X1 + 472 x2 + 298 X3 To maximize the number of calories burned, the man should spend 0 hours bicycling, 34 hours jogging, and 0 hours swimming (Simplify your answers.) He will burn a maximum of 16048 calories. (Simplify your answer.)