As shown in Figure $1,$ the density $(z)$ of the static fluid inside the tank is linear in the vertical

direction $z($i$.$e$.(z)=a+bz,$ where a and $b$ are known constants$).$ Gravity $g$ points in the

downward z$-$direction. The unit vector in the $y$ direction points into the paper. Attached to the

interior of the left wall is a suction cup, inside of which there is a vacuum, so the pressure inside

the suction cup is zero. The shape of the suction cup is quite irregular, and I have lost the equation

used to generate it$.$ However, I do know that the volume of the vacuum inside the suction cup has a

known value of $V.$ I also remember that the suction cup is symmetric with respect to the $x-y$ plane

at $z=0.($That is$,$ if we put a mirror in the $x-y$ plane at $z=0,$ the image of the top of the suction

cup in the mirror looks exactly like the bottom of the suction cup.$)$ I also know the values of $A_0,$

$A_2,$ and $A_3$ :

$A_0={\displaystyle \underset{S}{\overset{\phantom{}}{}}}dydz,A_2={\displaystyle \underset{S}{\overset{\phantom{}}{}}}{z}^{2}dydz,$ and $,A_3={\displaystyle \underset{S}{\overset{\phantom{}}{}}}{z}^{3}dydz$

where $S$ is that portion of the area of wall at $x=0$ that is exposed to the vacuum $($i$.$e$.,$ covered by

the suction cup$).$ Note that $A_0$ is the area of that portion of the left$-$edge wall that is covered by the

suction cup. Unfortunately, I cannot remember the value of

$A_1={\displaystyle \underset{S}{\overset{\phantom{}}{}}}zdydz$

Note that the force $F$ due to the pressure of the fluid acting on the suction cup is

$F={\displaystyle \underset{S^{\text{'}}}{\overset{\phantom{}}{}}}P(z)hat(n)d($ area $)$

where the integral is over the surface $S^{\text{'}}$ of the suction cup; the normal vector in the integrand is

inward normal unit vector from the fluid into the suction cup, and $P(z)$ is the pressure of the fluid

at height $z.$

Assume that the suction cup itself has no mass and that other than gravity, the pressure forces,

and the force from the left$-$hand edge of the tank acting on the fluid and on the suction cup, there

are no other forces in the system. The top of the tank is open to the atmosphere, which in this case

is $P_{\text{a}\text{t}\text{m}},$ but I cannot remember what the value of $z=z_0$ where the interface $($shown by the broken

line$)$ between the air and the fluid in the container is located. However, I do know that the pressure

in the fluid at $z=0$ is $P_0,$ whose value I know.

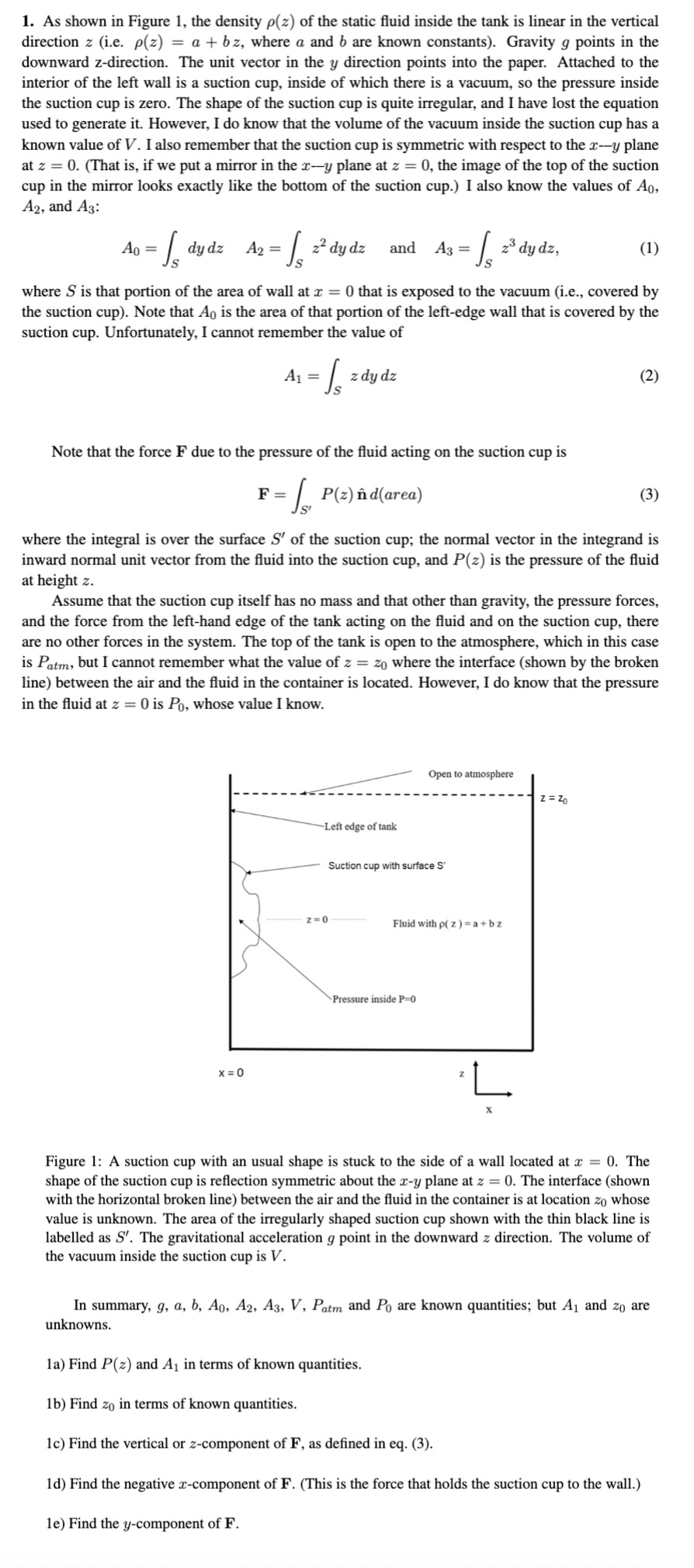
Figure $1$: A suction cup with an usual shape is stuck to the side of a wall located at $x=0.$ The

shape of the suction cup is reflection symmetric about the $x-y$ plane at $z=0.$ The interface $($shown

with the horizontal broken line$)$ between the air and the fluid in the container is at location $z_0$ whose

value is unknown. The area of the irregularly shaped suction cup shown with the thin black line is

labelled as $S^{\text{'}}.$ The gravitational acceleration $g$ point in the downward $z$ direction. The volume of

the vacuum inside the suction cup is $V.$

In summary, $g,a,b,A_0,A_2,A_3,V,P_{\text{a}\text{t}\text{m}}$ and $P_0$ are known quantities; but $A_1$ and $z_0$ are

unknowns.

$1$a$)$ Find $P(z)$ and $A_1$ in terms of known quantities.

$1$b$)$ Find $z_0$ in terms of known quantities.

$1$c$)$ Find the vertical or $z-$component of $F,$ as defined in eq$.(3).$

$1$d$)$ Find the negative $x-$component of $F.($This is the force that holds the suction cup to the wall.$)$

$1$e$)$ Find the $y-$component of $F.$

please give a clear explanation and formulas!