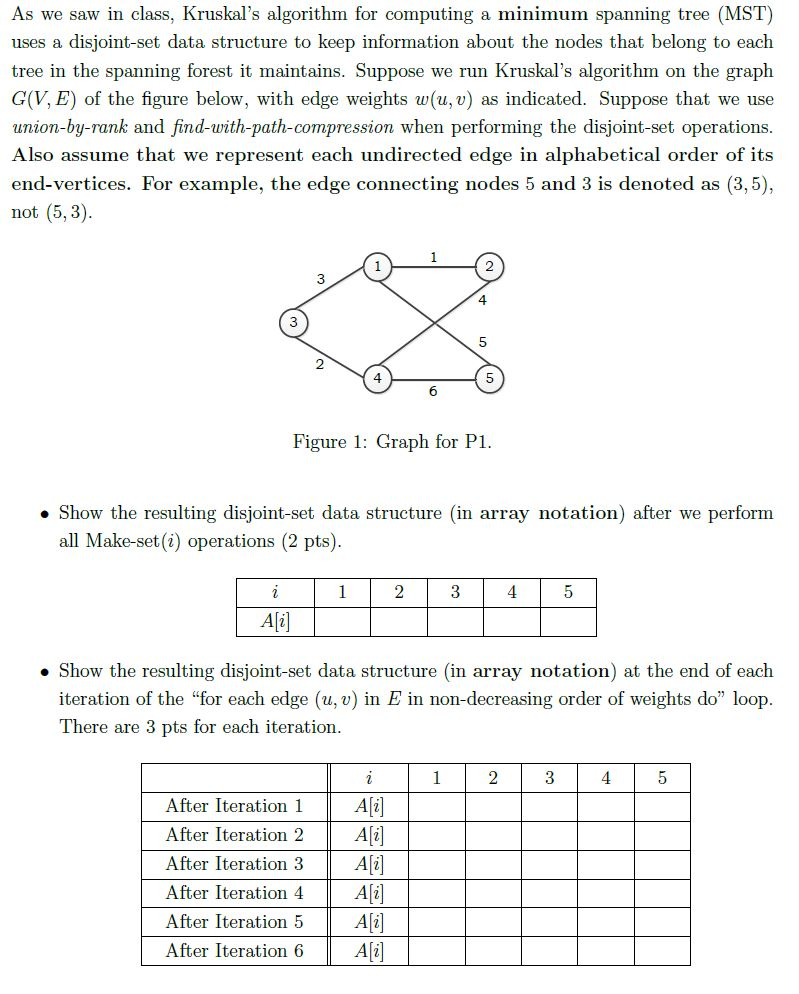
As we saw in class, Kruskal's algorithm for computing a minimum spanning tree (MST) uses a disjoint-set data structure to keep information about the nodes that belong to each tree in the spanning forest it maintains. Suppose we run Kruskal's algorithm on the graph G(V, E) of the figure below, with edge weights w(u, v) as indicated. Suppose that we use union-by-rank and find-with-path-compression when performing the disjoint-set operations Also assume that we represent each undirected edge in alphabetical order of its end-vertices. For example, the edge connecting nodes 5 and 3 is denoted as (3,5), not (5, 3) 4 5 2 4 6 Figure 1: Graph for P1. Show the resulting disjoint-set data structure (in array notation) after we perform all Make-set (i) operations (2 pts) Ali . Show the resulting disjoint-set data structure (in array notation) at the end of each iteration of the "for each edge (u, v) in E in non-decreasing order of weights do" loop There are 3 pts for each iteration 4 After IterationA After Iteration 2 Ai After Iteration 3Ai After Iteration 4 A After Iteration 5 A] After Iteration 6Ai] As we saw in class, Kruskal's algorithm for computing a minimum spanning tree (MST) uses a disjoint-set data structure to keep information about the nodes that belong to each tree in the spanning forest it maintains. Suppose we run Kruskal's algorithm on the graph G(V, E) of the figure below, with edge weights w(u, v) as indicated. Suppose that we use union-by-rank and find-with-path-compression when performing the disjoint-set operations Also assume that we represent each undirected edge in alphabetical order of its end-vertices. For example, the edge connecting nodes 5 and 3 is denoted as (3,5), not (5, 3) 4 5 2 4 6 Figure 1: Graph for P1. Show the resulting disjoint-set data structure (in array notation) after we perform all Make-set (i) operations (2 pts) Ali . Show the resulting disjoint-set data structure (in array notation) at the end of each iteration of the "for each edge (u, v) in E in non-decreasing order of weights do" loop There are 3 pts for each iteration 4 After IterationA After Iteration 2 Ai After Iteration 3Ai After Iteration 4 A After Iteration 5 A] After Iteration 6Ai]