Assignment 3B testing a User Defined Combo ADT

Purpose

This assignment is to exercise one of the basic container class: List, Stack and Queue in Chapter 7, 8, 9, 13 and 14 of the Carrano textbook.

We are going to use the NumberList Class that we templated in Module 2 ( source code can be found in the mo2/test_NumberList.cpp) as a base and design a generic Combo (Stack + Queue) Class.

You may use the textbook Chapter 14 example and exercise on design and apply the C++ class.

Designing a Combo (Stack + Queue) Class

Before you start on this exercise, you must be pretty familiar with the templating of a specific typed container. We have covered that topic in Module 2. Let us assume everyone is really comfortable in converting a typed linked list to a generic template linked list.

We are going to add the following class methods by adding/modifying necessary code to the LinkedLList class from the Module 2. We are going to complete the following Combo features mapped from the STL Stack and Queue:

STL Stack	STL Queue	Combo Container
empty	empty	empty
size	size	size
top	front	front
back		back
	push	push_front
push		push_back
pop	pop	pop_front
		pop_back

Complete all combo class feature methods listed above.

Create a toString() method to output a string of the all nodes' value separated by a space character.

Use the provided test driver to validate your work.

Convert this test driver software into an user interactive with batch capability test program.

Defined below is the Combo container class definition. Some NumberList class methods are commented out but left there for your reference. You may also find the following source code in the starter m03/as3_Combo_starter.cpp and the original NumberList Class m02/test_list.cpp at the course github.

template struct Node { T value; // The value in this node Node *next; // To point to the next node }; template class Combo { private: int count; Node *head; // List head pointer public: // Constructor Combo() { head = nullptr; count = 0; } // Destructor ~Combo() { Node *p = head; while(p) { delete p; p = p->next; } } // void insert(T); // ref. for push_front // void remove(T); // ref. for pop_front and pop_back // void display() const; // use for initial debug, then removed std::string toString(); // here are the Combo Stack & Queue features T front(); // read front T back(); // read back void push_front(T); void push_back(T); // i.e append void pop_front(); void pop_back(); int size() { return count; } }; 

Test Run

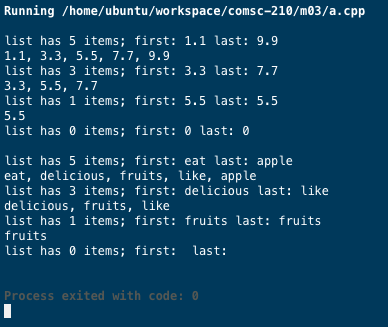
we are going to create a user interface that when program runs, its execution would look like the following screen capture:

int main() { Combo list; list.push_front(3.3); list.push_front(1.1); list.push_back(5.5); list.push_back(7.7); list.push_back(9.9); auto showd = [](Combo& x) { cout  
Test Run Sample Result
 
 
Submit
 
as3_testCombo.cpp
 
Including the Combo Container class declaration and definition
 
 
 
Assignment 4 Postfix Calculator
 
The stack based calculator is constructed using the postfix notation. In this assignment, we are to implement the postfix calculator using the Stack and Queue from the Combo class that we build previously.
 
We are to create one queue to hold all input tokens and one stack for hold the operands. The calculation shall follow the depicted description above.
 
This program shall not check the validity of the postfix expression. It is assumed that the test pattern is valid. Use this online infix to postfix converter (Links to an external site.)Links to an external site. to generate a valid postfix expression from infix expression for your choice.
 
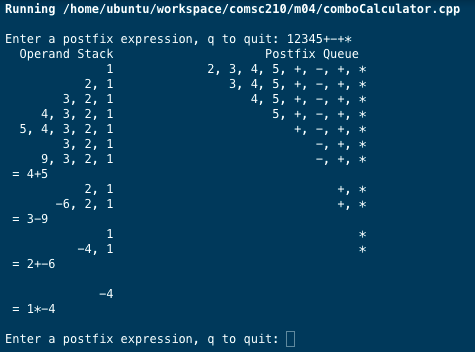
Your program shall implement and show:
 
the user input 
 
the calculation of following 5 operators: + - * / ^
 
tracing of all the content of the Operand Stack and Postfix Queue between changes.
 
Sample Test Output
 
For this exercise we are to use a line prompt for user to enter a postfix expression. 
 
 
 
 
 
 
 
Submit
 
comboCalculator.cpp
 
The postfix Calculator application with the Combo class.
 
Reference 4 Infix Calculator
 
In this exercise, we are to add an Infix to Postflix processor to the Postfix Calculator implemented in Lab 4. 
 
Converting Infix to Postfix
 
The postfix notation, also called the Reverse Polish notation (RPN) is a mathematical notation in which every operator follows all of its operands. For instance, to add 3 and 4, one would write "3 4 +" rather than "3 + 4", infix notation. We shall learn the conversion algorithm between different notations. Here are the reference (wiki) documents:
 
reverse polish notation wiki (Links to an external site.)Links to an external site.
 
operator associativity wiki (Links to an external site.)Links to an external site.
 
infix to postfix conversion wiki (Links to an external site.)Links to an external site.
 
The following lists our assumptions on the mathematical expression entered by the user:
 
The mathematical expression in infix notation is a valid one (e.g. 1 + 23 is valid while 1 +2 is not; or 5 is valid while +34 / is not).
 
The operands of the given mathematical expression are integers from 0 to 9 only.
 
The only allowable operators are + (for addition),  (for subtraction),  (for multiplication), / (for division), and  (for exponentiation). Negative sign is not allowed.
 
Division by zero is not allowed.
 
The exponentiation operator has the highest precedence followed by the multiplication and division operators and finally the addition and subtraction operators.
 
The exponentiation operator is right-associative while all the other operators are left-associative.
 
Parentheses can appear in the mathematical expression.
 
Parentheses can be nested.
 
Assume that the parentheses are well-balanced.
 
Blank spaces can appear in the mathematical expression.
 
There is no limit as to the length of the mathematical expression.
 
The input is terminated when the user hits the ENTER key.
 
 
 
In this Assignment, we are to add the Infix to Postfix conversion function to preprocess the user input to a postfix string for the Postfix Calculator.
 
The purpose of this assignment is to become familiar with solving real life problem with different C++ STL containers. I will be using a Operator Stack and a output Postfix Queue to solve this problem. There are many ways to solve this problem, you are encouraged to try different ADT.
 
In your finished program you shall show the content of the Infix Stack and Postfix Queue during the conversion step by step, as shown in the sample test below.
 
Sample Test
 
 
 
In your validation all five arithmetic operators shall be tested.
  Running /home/ubuntu/workspace/comsc-210/m03/a.cpp list has 5 items; first: 1.1 last: 9.9 1.1, 3.3, 5.5, 7.7, 9.9 list has 3 items; first: 3.3 last: 7.7 3.3, 5.5, 7.7 list has 1 items; first: 5.5 last: 5.5 5.5 list has0 items; first: 0 last: 0 list has 5 items; first: eat last: apple eat, delicious, fruits, like, apple list has 3 items; first: delicious last: like delicious, fruits, like list has 1 items; first: fruits last: fruits fruits list has 0 items; first: last: Process exited with code