Question: Assignment 6 1 Question 1: Verify that y = 623 is a solution of the differential equation 3; + yr 23; = U. {6 points)

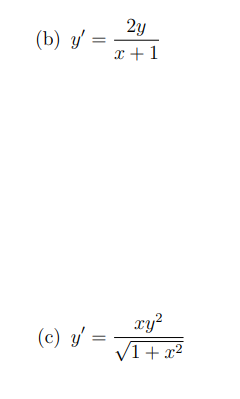

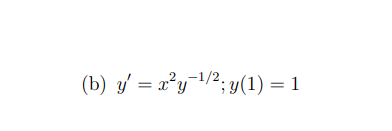
![solution of the following initialvalue problem. (12 points] {a} y' = aley;](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661fbc79d0fd_4796661fbc784878.jpg)
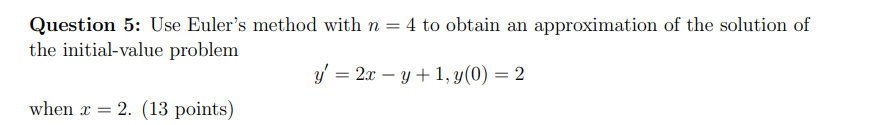

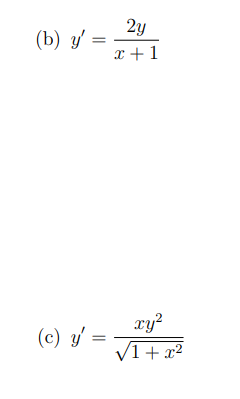

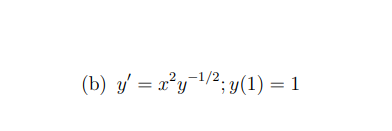
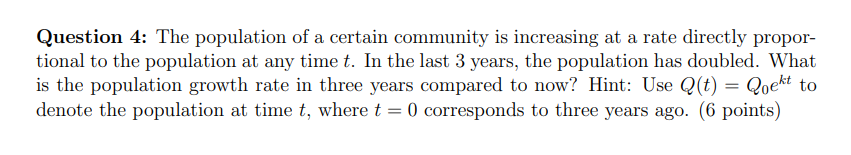
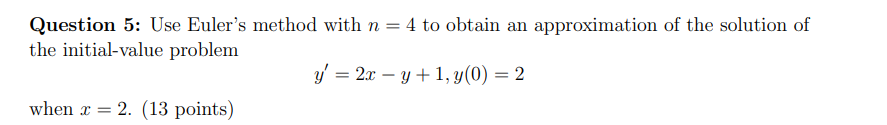
Assignment 6 1 Question 1: Verify that y = 623 is a solution of the differential equation 3;" + yr 23; = U. {6 points) Question 2: Solve the rst order differential equation by separating variables. [18 points) (a) if = 2(1: -1} Question 3: Find the solution of the following initialvalue problem. (12 points] {a} y' = aley; y(} = 1 Question 4: The population of a certain community is increasing at a rate directly propor tional to the population at any time t. In the last 3 years, the population has doubled. "That is the population growth rate in three years compared to now? Hint: Use Q[t) = Q08" to denote the population at time t, where t = (II corresponds to three years ago. (6 points) Question 5: Use Euler's method with n = 4 to obtain an approximation of the solution of the initial-value problem y' = 2x - y + 1, y(0) = 2 when x = 2. (13 points)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


