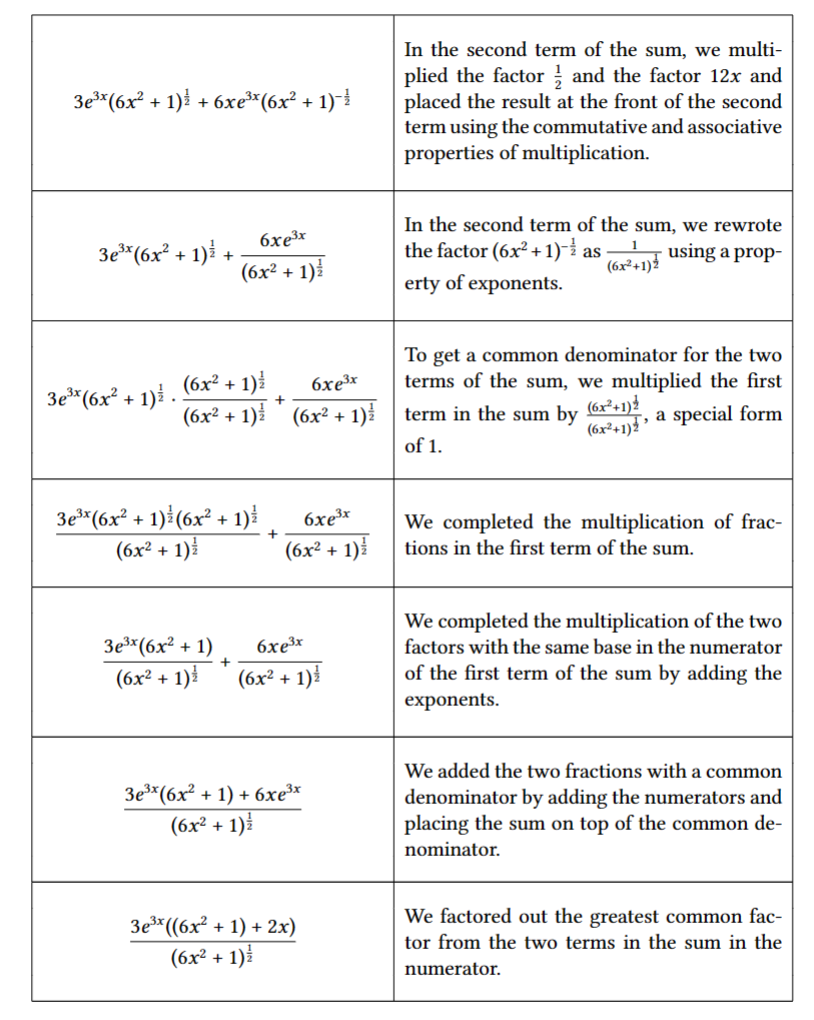
Assignment: Algebraically manipulate the following expression: (1) Ex) e+ (k2 -1)" e e Include a detailed explanation for each mathematical step written in grammatically correct com- plete sentences within a 2-column format. Your final answer should follow these guidelines: + Completely factored Reduced into lowest terms Single quotient + Only positive exponents and roots Sample Problem and Solution: Problem: Algebraically manipulate the following expression: 3 (622 + 1)} + (%) (6x% + 1)} (12x). Answer: 3e*(6x2 + 2x + 1) (6x2 + 1): Solution: This is the expression we were given to ma- nipulate. 3 (6x% + 1)7 + (1) (6x% + 1)73(12x) 33X (6x% + 1)% + 6xe>(6x + 1)} 6xe'* 3e*(6x + l)% g (6x% +1)2 6xe' Fr (6x%+1): 6xe'* (6x% + 1)z 3e3%(6x% + 1) (6x% + 1) (6x% + 1)2 3e**(6x% + 1) 6xe* (6x2+1)F (6x2 + 1)} 3 (6x% + 1) + 6xe* (6x% +1): 3' ((6x% + 1) + 2x) (6x% + 1): In the second term of the sum, we multi- plied the factor ; and the factor 12x and placed the result at the front of the second term using the commutative and associative properties of multiplication. In the second term of the sum, we rewrote | 1 . 3 the factor (6x*+1)"z as m using a prop erty of exponents. To get a common denominator for the two terms of the sum, we multiplied the first term in the sum by %&, a special form of 1. We completed the multiplication of frac- tions in the first term of the sum. We completed the multiplication of the two factors with the same base in the numerator of the first term of the sum by adding the exponents. We added the two fractions with a common denominator by adding the numerators and placing the sum on top of the common de- nominator. We factored out the greatest common fac- tor from the two terms in the sum in the numerator. We rearranged the terms in the second fac- tor in the numerator using the commutative property of addition. Since the second fac- tor in the numerator cannot be factored and 3e3(6x% + 2x + 1) (6x2 + 1)z the fraction cannot be reduced, we are done. Check List: O Did you show every mathematical step? O Did you proofread your work to make sure all of your mathematical steps are correct? O Did you use words to fully explain all of your mathematical steps? o Did you proofread your writing to make sure you used complete sentences and correct grammar? o Does your work on this problem create a complete and cohesive story? (Q - (x - 1 ) ( 2x ) ex + (2 -1 ) ex This is the expression we were ex given to manipulate. & l - (2- 1) ( 2x ) + (x- 151 ) take ex as common from Rumerator and dluside it with denomination = - (x - 1) (2 * ) + (x21) - In first term of the sum, we rewrote the factor (2-152 as - 2x + ( x 2 - 1 1 2 ( * 2 ( x 2 _ 1 1 2 and in second term. - 1) (x 2-1)' using a * 2 - 1 proporty of exponents. 2y To get common denominator + for two terms of the sum, ( x - 1 ) X2 1 we multiplied second term with - 2 * + ( x2- 1 ) * 2 -1 1 2- 1 a special form of 1 ( X 2 - 1 1 2 Given * - 2 x + ( 1 ) we factored out the greatest problem. ( X 2 - 1 )2