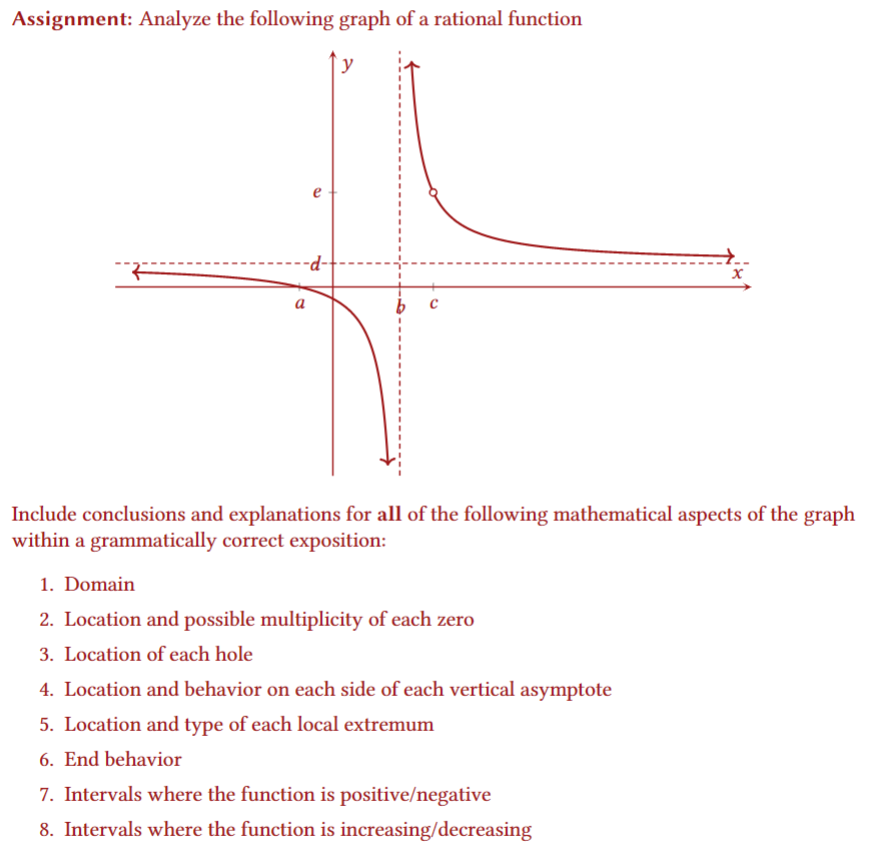
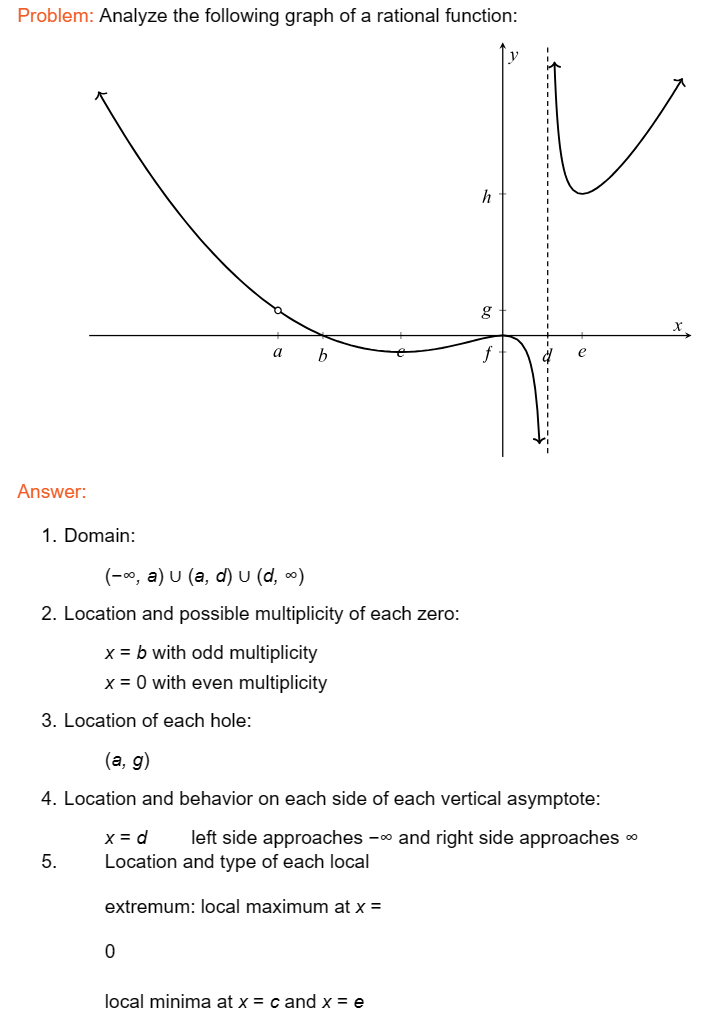
Assignment: Analyze the following graph of a rational function decscccsancscscccaanacaanas e mm s e e et = Include conclusions and explanations for all of the following mathematical aspects of the graph within a grammatically correct exposition: 1. = = I - R Domain . Location and possible multiplicity of each zero . Location of each hole . Location and behavior on each side of each vertical asymptote . Location and type of each local extremum . End behavior . Intervals where the function is positiveegative . Intervals where the function is increasing/decreasing Problem: Analyze the following graph of a rational function: e e e e e s e L o Answer: 1. Domain: (==, a) U (a, d) U (d, ) 2. Location and possible multiplicity of each zero: x = b with odd multiplicity x = 0 with even multiplicity 3. Location of each hole: (a, 9) 4. Location and behavior on each side of each vertical asymptote: x=d left side approaches = and right side approaches = 5. Location and type of each local extremum: local maximum at x = 0 local minima atx=cand x=e 6. End behavior: as x = the rational function approaches % as x = the rational function approaches no horizontal asymptote 7. Intervals where the function is positiveegative: positive on (==, a) U (a, b) U (d, =) negative on (b, 0) U (0, d) 8. Intervals where the polynomial is increasing/decreasing: increasing on (, 0) U (e, =) decreasing on (-=, a) U (a, c) U (0, d) U (d, e) Solution: The domain of the rational function is (-, a) U (a, d) U (d, =). We can see this on the graph by noticing that the only two places where the rational function is not defined are at x = a and x = d. The rational function has zeros located at x = b and x = 0. At x = b, the graph crosses the x-axis, implying that the multiplicity of the zero must be odd. At x = 0, the graph touches the x-axis but does not cross it, implying that the multiplicity of the zero must be even. The rational function has a hole located at (a, g) since a single point is removed from the graph there. If this point was filled in, the rational function would be continuous at x =a. The rational function has a vertical asymptote at x = d. Looking to the left of the vertical asymptote, the function decreases without bound, so the rational function approaches - on the left side of the vertical asymptote. Looking to the right of the vertical asymptote, the function increases without bound, so the rational function approaches on the right side of the vertical asymptote. The rational function has local extrema located at x = , x=0,and x = e. At x = 0, the function has a local maximum because the function value is bigger there than any other function value nearby. At both x = and at x = e, the function has a local minimum because at those two places, the function value is smaller than any other function value nearby. To assess the end behavior of the rational function, we must consider what is happening to the graph as x approaches negative infinity and as x approaches positive infinity. As x approaches both negative infinity and positive infinity, the graph of the rational function goes up without bound. So, the end behavior tends to infinity as x approaches both negative infinity and positive infinity. Since the end behavior is not finite, the rational function does not have a horizontal asymptote. The positive and negative intervals of the rational function are separated by the zeros within the domain of the function. We conclude that the rational function is positive whenever the graph is above the x-axis, and we conclude that the rational function is negative whenever the graph is below the x-axis. So, starting on the left side of the graph and working our way to the right, we see that the rational function is positive on (-=, a), remains positive on (a, b), changes to negative on (b, 0), remains negative on (0, d), and changes to positive on (d, ). The increasing and decreasing intervals of the rational function are separated by the extrema within the domain of the function. We conclude that the rational function is increasing whenever the graph is going up as we move from left to right, and we conclude that the rational function is decreasing whenever the graph is going down as we move from the left to the right. So, starting on the left side of the graph and working our way to the right, we see that the rational function is decreasing on (-, a), remains decreasing on (a, ), changes to increasing on (, 0) and then back to decreasing on (0, d), remains decreasing on (d, e), and changes to increasing on (e, ). Check List: Did you analyze all requested mathematical aspects of the graph? Did you proofread your work to make sure all of your mathematical steps are correct? o Did you use words to fully explain all of your mathematical steps? Did you proofread your writing to make sure you used complete sentences and correct grammar? Does your work on this problem create a complete and cohesive story? Grading Rubric: Mathematical Steps Written Justifications T o All'steps are accompanied by correct and Exemplary (10 points) All steps are complete justifications included and correct Nearly all steps are accompanied by Proficient (9 points) Nearly all steps correct and complete justifications are included Steps are generally accompanied by and correct correct and complete justifications Competent (7 points) Steps are Several steps have missing and/or in- generally included complete justifications and correct Many steps have missing and/or in- Developing (5 points) Several steps are complete justifications missing and/or incorrect Beginning (2 points) Many steps are missing and/or incorrect