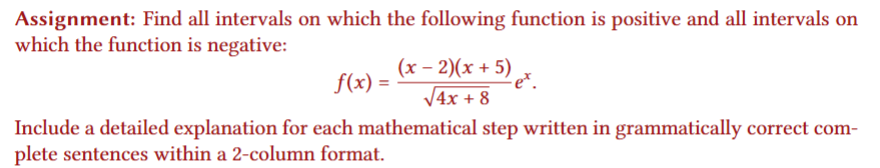
Assignment: Find all intervals on which the following function is positive and all intervals on which the function is negative: ) = (x=2)(x+ 5)81 Jax+8 ) Include a detailed explanation for each mathematical step written in grammatically correct com- plete sentences within a 2-column format. Sample Problem and Solution: Problem: Find all intervals on which the following function is positive and all intervals on which the function is negative: (x+3)Ja-x f)= x*(x = 5) Answer: Positive: (oo, -3) Negative: (-3,0) u (0,4) Solution: This is the function we were given. Notice that it is already in factored form. = = v I X X x=5 # x N 0 4 (x+3)Va-x 0 x+3 0 X -3 Vi -x 0 4-x 0 4 x X 1 We began by determining where f(x) is de- fined and where it is undefined. Since f(x) has a factor that is an even root, we know that we can only have numbers bigger than or equal to zero under the even root. Fur- thermore, since f(x) is a fraction, we know that we can only have non-zero numbers in the bottom of the fraction. Combining this information, we can plot the domain of f(x) on the number line. Next we determine all places within the do- main of f(x) that f(x) = 0. This happens whenever the top of the fraction is equal to zero, and to solve that equation, we set each individual factor equal to zero and solve those equations. Note that each of the so- lutions is in the domain of f(x), so f(x) has zeros at x = -3 and x = 4. The zero x = 4 is already plotted on the number line since it is the edge of the do- main, so we add the other zero x = -3 to the number line. Positive: (o0, -3) Negative: (-3,0) u (0,4) Next we choose a test value in each interval to help us determine the sign of each inter- val. We indicate these test values in paren- theses since they are not uniquely chosen. First note that the factor V4 - x and the fac- tor x* are both positive on every interval, so it remains to determine the sign of the fac- tor x+3 and the factor x-5 for each interval. For the test value 4, the factor x + 3 is neg- ative and the factor x - 5 is negative. That gives us a positive value overall for that in- terval. For the test value -1, the factor x + 3 is positive and the factor x - 5 is negative. That gives us a negative value overall for that interval. For the test value 1, the factor x + 3 is positive and the factor x - 5 is nega- tive. That gives us a negative value overall for that interval. With the sign of each interval determined, we can now use interval notation to provide the intervals on which f(x) is positive and on which f(x) is negative