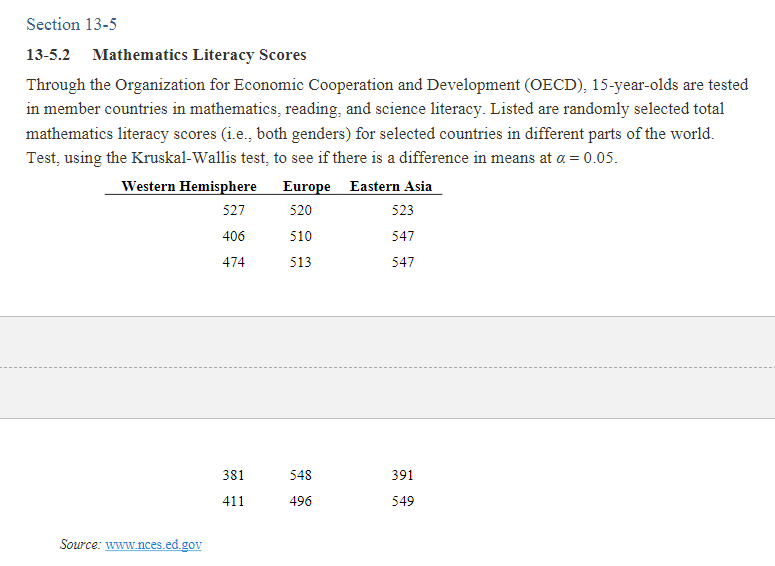
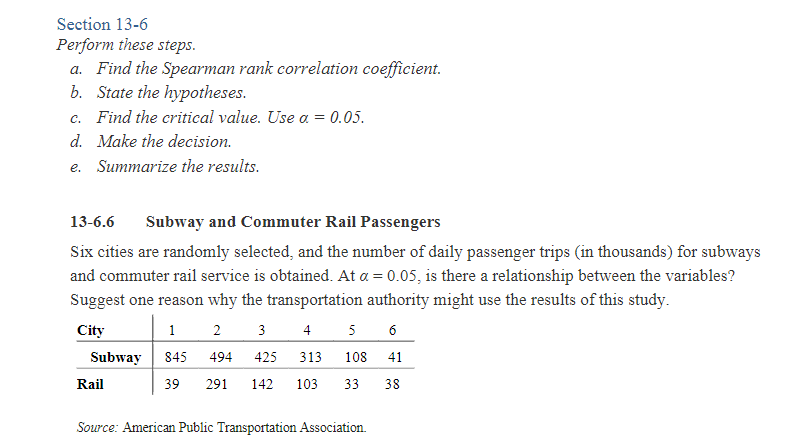
Assignment Summary Complete the following problems using R. Be sure to show your work and include the hypothesis tests, the critical values, the computed test values, and the resulting decisions where applicable. Section 13-2 13-2.6 Game Attendance An athletic director suggests the median number for the paid attendance at 20 local football games is 3000. The data for a random sample are shown. At = 0.05, is there enough evidence to reject the claim? If you were printing the programs for the games, would you use this figure as a guide? 6210 3150 2700 3012 4875 3540 6127 2581 2642 2573 2792 2800 2500 3700 6030 5437 2758 3490 2851 2720 Source: Pittsburgh Post Gazette. 13-2.10 Lottery Ticket Sales A lottery outlet owner hypothesizes that she sells 200 lottery tickets a day. She randomly sampled 40 days and found that on 15 days she sold fewer than 200 tickets. At = 0.05, is there sufficient evidence to conclude that the median is below 200 tickets? Section 13-3 Use the Wilcoxon rank sum test. 13-3.4 Lengths of Prison Sentences A random sample of men and women in prison was asked to give the length of sentence each received for a certain type of crime. At = 0.05, test the claim that there is no difference in the sentence received by each gender. The data (in months) are shown here. Males 8 12 6 14 22 27 32 24 26 Females 7 5 2 3 21 26 30 9 4 Males 19 15 13 Females 17 23 12 11 16 Source: Based on information from the National Highway Traffic Safety Administration. 13-3.8 Winning Baseball Games For the years 1970-1993 the National League (NL) and the American League (AL) (major league baseball) were each divided into two divisions: East and West. Below are random samples of the number of games won by each league's Eastern Division. At = 0.05, is there sufficient evidence to conclude a difference in the number of wins? NL 89 96 88 101 90 91 92 96 108 100 95 AL 108 86 91 97 100 102 95 104 95 89 88 101 Source: World Almanac. Section 13-4 13-4.A Use Table K (or relevant software) to determine whether the null hypothesis should be rejected. w=13, n = 15, a = 0.01, two-tailed ws=32, n = 28, a = 0.025, one-tailed ws=65, n = 20, = 0.05, one-tailed ws = 22, n = 14, a = 0.10, two-tailed Section 13-5 13-5.2 Mathematics Literacy Scores Through the Organization for Economic Cooperation and Development (OECD), 15-year-olds are tested in member countries in mathematics, reading, and science literacy. Listed are randomly selected total mathematics literacy scores (i.e., both genders) for selected countries in different parts of the world. Test, using the Kruskal-Wallis test, to see if there is a difference in means at = 0.05. Western Hemisphere Source: www.nces.ed.gov Europe Eastern Asia 527 520 523 406 510 547 474 513 547 381 548 391 411 496 549 Section 13-6 Perform these steps. a. Find the Spearman rank correlation coefficient. b. State the hypotheses. c. Find the critical value. Use = 0.05. d. Make the decision. e. Summarize the results. 13-6.6 Subway and Commuter Rail Passengers Six cities are randomly selected, and the number of daily passenger trips (in thousands) for subways and commuter rail service is obtained. At = 0.05, is there a relationship between the variables? Suggest one reason why the transportation authority might use the results of this study. 1 2 3 4 5 6 City Subway 845 494 425 313 108 41 Rail 39 291 142 103 33 38 Source: American Public Transportation Association. Section 14-3 Use random numbers to simulate the experiments. The number in parentheses is the number of times the experiment should be repeated. 14-3.16 Prizes in Caramel Corn Boxes A caramel corn company gives four different prizes, one in each box. They are placed in the boxes at random. Find the average number of boxes a person needs to buy to get all four prizes. (40) 14-3.18 Lottery Winner To win a certain lotto, a person must spell the word big. Sixty percent of the tickets contain the letter b, 30% contain the letter i, and 10% contain the letter g. Find the average number of tickets a person must buy to win the prize. (30)