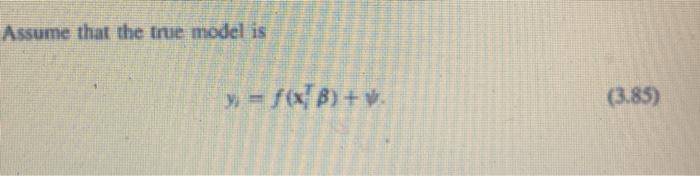
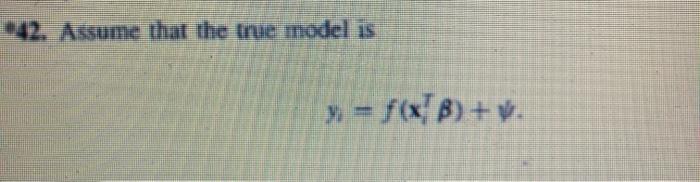
Assume that the true model is y = f(x+B) + (3.85) Transforming y to f'() would allow the transformed response to be represented approximately by a linear model. The nonlinearity in (3.85) is referred to as transformable non-additivity. Suppose that the usual linear y Be (3.86) is fitted to the data. Letting u B. a Taylor series approximation yields f(a) ~ Yu + 224 (387) where y and nu are constants. Does (3.87) suggest that is an important covariate of y? What would a plot of 9 versus n look like? [Hint Compare (386) and (3.87).) 42. Assume that the true model is y = f(x) + . Transforming y to f-'(y) would allow the transformed response to be represented approximately by a linear model. The nonlinearity in (3.85) is referred to as transformable now additivin. Suppose that the usual linear model y = x + (3.86) is fitted to the data. Letting p1 - x'B. a Taylor series approximation yields f(a) ~ + ?. 0.87) where. n and n are constants. Does (3.87) suggest that it is an important covariate of y? What would a plot of 9 versus r, look like? [Hint: Compare (3.86) and (3.87).] Assume that the true model is y = f(x+B) + (3.85) Transforming y to f'() would allow the transformed response to be represented approximately by a linear model. The nonlinearity in (3.85) is referred to as transformable non-additivity. Suppose that the usual linear y Be (3.86) is fitted to the data. Letting u B. a Taylor series approximation yields f(a) ~ Yu + 224 (387) where y and nu are constants. Does (3.87) suggest that is an important covariate of y? What would a plot of 9 versus n look like? [Hint Compare (386) and (3.87).) 42. Assume that the true model is y = f(x) + . Transforming y to f-'(y) would allow the transformed response to be represented approximately by a linear model. The nonlinearity in (3.85) is referred to as transformable now additivin. Suppose that the usual linear model y = x + (3.86) is fitted to the data. Letting p1 - x'B. a Taylor series approximation yields f(a) ~ + ?. 0.87) where. n and n are constants. Does (3.87) suggest that it is an important covariate of y? What would a plot of 9 versus r, look like? [Hint: Compare (3.86) and (3.87).]