Assume that you observe the random sequence Y (n), generated via:

Y (n) = 2X(n) + N(n) (1)

where X(n) is the original sequence of signals; N(n) is the noise sequence; X(n),n = 1,2,... and N(n),n = 1,2,... are i.i.d, unit variance Gaussian random variables;

X(n) is zero mean and N(n) has a mean of 0.3.

Problem 1.(a) [10 points] Compute from eqn (1), the correlation coefficient ? X(n)Y (n) .

Problem 1.(b) [10 points] Using eqn. 6.55,

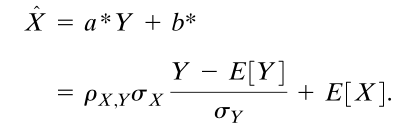
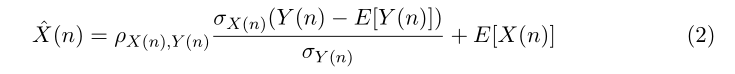
\f\f\f