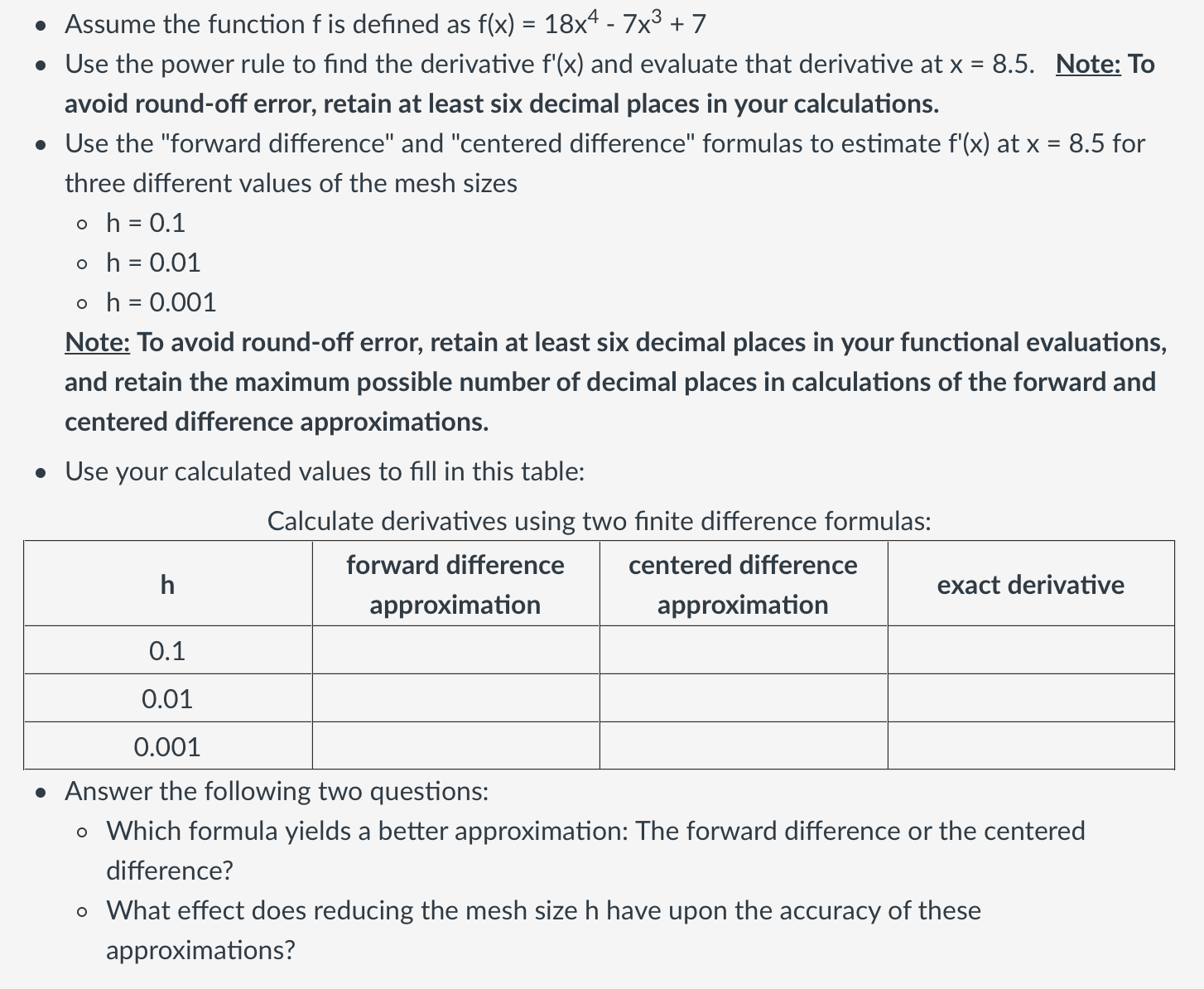
. Assume the function f is defined as f(x) = 18x4 - 7x3 + 7 . Use the power rule to find the derivative f'(x) and evaluate that derivative at x = 8.5. Note: To avoid round-off error, retain at least six decimal places in your calculations. . Use the "forward difference" and "centered difference" formulas to estimate f'(x) at x = 8.5 for three different values of the mesh sizes oh = 0.1 o h = 0.01 o h = 0.001 Note: To avoid round-off error, retain at least six decimal places in your functional evaluations, and retain the maximum possible number of decimal places in calculations of the forward and centered difference approximations. . Use your calculated values to fill in this table: Calculate derivatives using two finite difference formulas: h forward difference centered difference exact derivative approximation approximation 0.1 0.01 0.001 . Answer the following two questions: o Which formula yields a better approximation: The forward difference or the centered difference? o What effect does reducing the mesh size h have upon the accuracy of these approximations