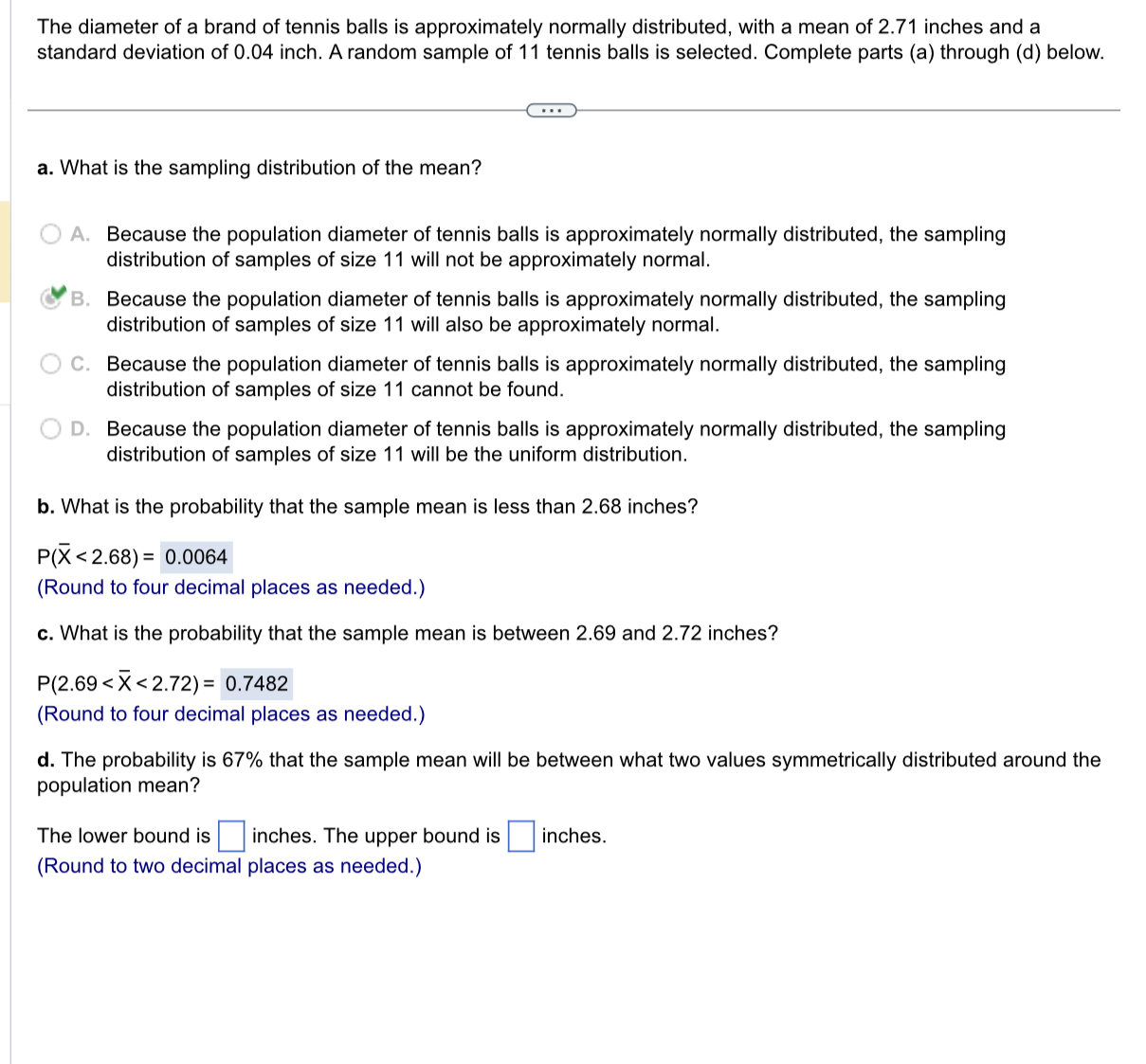
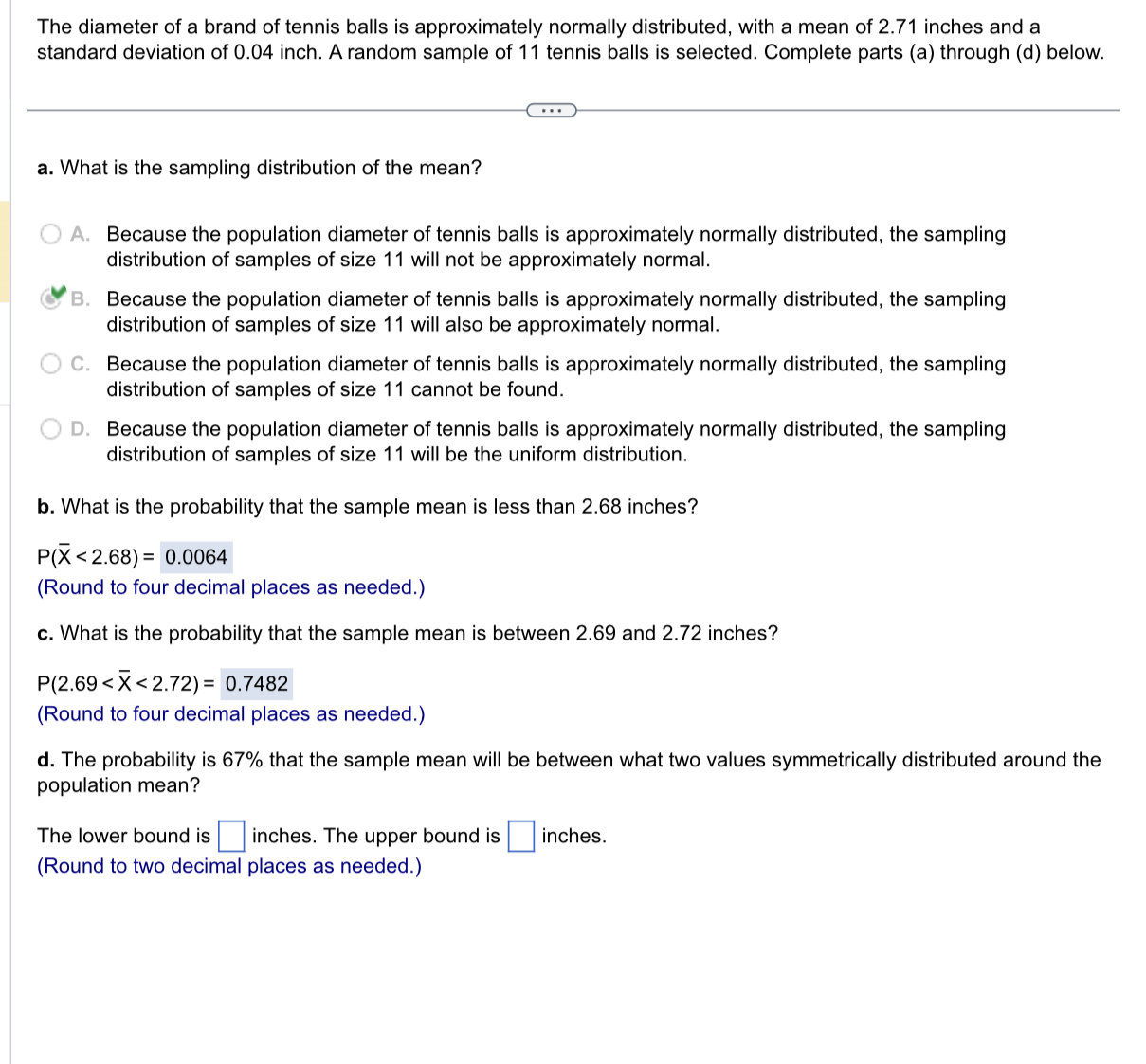
Assuming that the population is normally distributed, construct a 95% confidence interval for the population mean for each of the samples below. Explain why these two samples produce different confidence intervals even though they have the same mean and range. Sample A: 1 2 2 2 7 7 7 8 Full data set Sample B: 1 2 3 4 5 6 7 8 . . . Construct a 95% confidence interval for the population mean for sample A. 2.01 Sus 6.99 (Type integers or decimals rounded to two decimal places as needed.) Construct a 95% confidence interval for the population mean for sample B. SHS (Type integers or decimals rounded to two decimal places as needed.)Given a normal distribution with 1.1 = 103 and c = 25. and given you select a sample of n = 25. complete parts (a) through (d). a. What is the probability that >_( is less than 92? P()_( 104.6) = 03745 (Type an integer or decimal rounded to four decimal places as needed.) d. There is a 61% chance that )_( is above what value? m (Type an integer or decimal rounded to two decimal places as needed.) The diameter of a brand of tennis balls is approximately normally distributed, with a mean of 2.71 inches and a standard deviation of 0.04 inch. A random sample of 1 1 tennis balls is selected. Complete parts (a) through (d) below. {:3- a. What is the sampling distribution of the mean? Because the population diameter of tennis balls is approximately normally distributed, the sampling distribution of samples of size 11 will not be approximately normal. V Because the population diameter of tennis balls is approximately normally distributed. the sampling distribution of samples of size 11 will also be approximately normal. Because the population diameter of tennis balls is approximately normally distributed, the sampling distribution of samples of size 11 cannot be found. Because the population diameter of tennis balls is approximately normally distributed. the sampling distribution of samples of size 11 will be the uniform distribution. b. What is the probability that the sample mean is less than 2.68 inches? Po?