Attached 3 questions with the evaluation method 1 & 2.

Remember to state the reason if one of the evaluation method cannot be used.

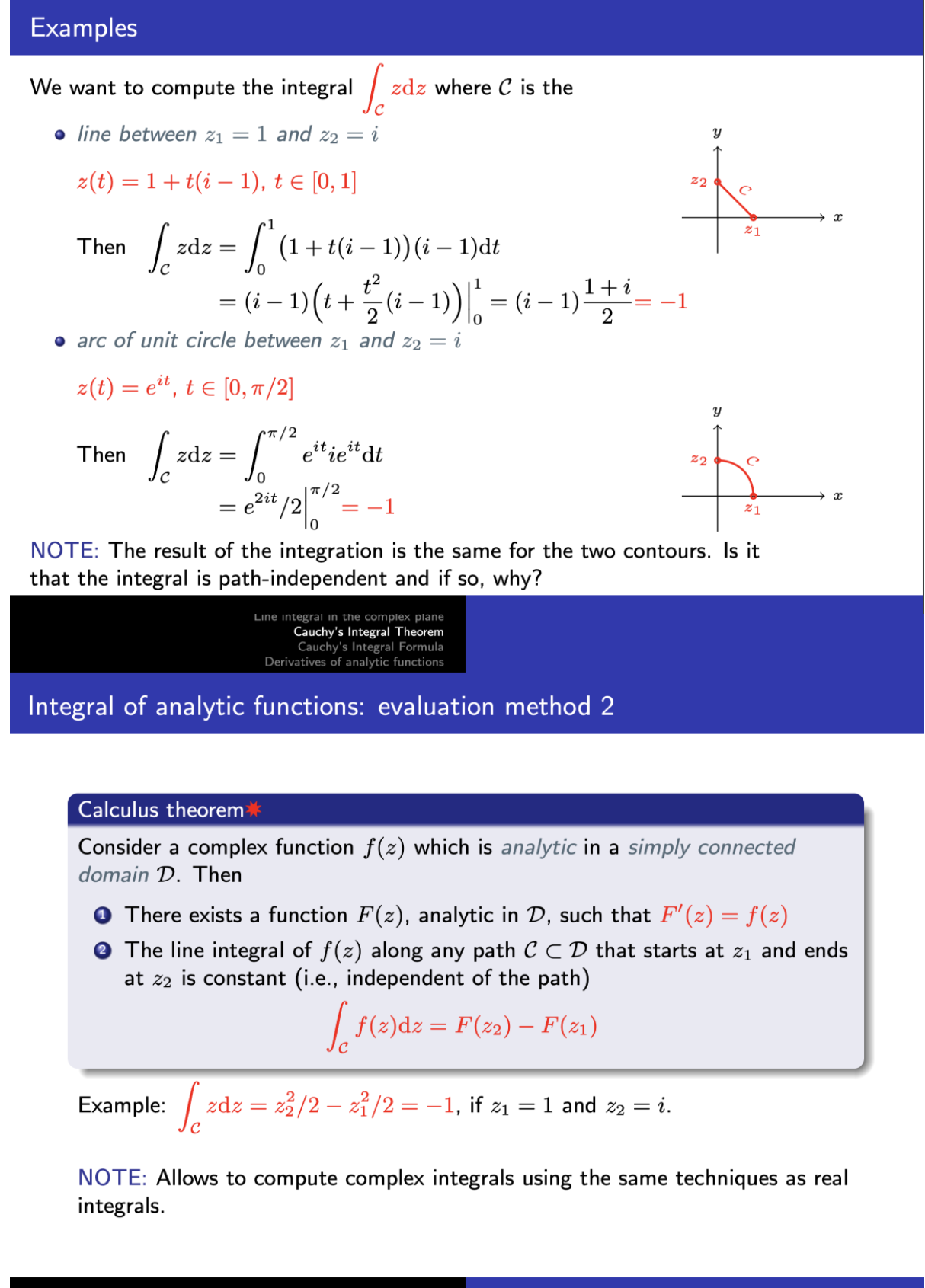
Complex integration: evaluation method 1 Path integral# Given a smooth directed curve C oriented from z(a) to z(b), and f(z) defined on C This definition is extended to directed contours. When the contour is closed, the integral is denoted by of f(z) dz. 2(t) f ( z (t) ) z(t + At) - z(t) z(t + At) z (t ) 0 NOTE: In general, the integral depends on the path/contour chosen, but not on the parametrization. Line integral in the complex plane Cauchy's Integral Theorem Cauchy's Integral Formula Derivatives of analytic functions Examples We want to compute the integral zdz where C is the . line between z1 = 1 and z2 = i z(t) = 1+t(i - 1), te [0, 1] Z2 9 Then [ Edz = [ ( 1 + + (-i-1) (1-1)at 21 = (2 - 1)(t - 2(2+1)) 12= (i-1)1-2=i . arc of unit circle between z1 and z2 = i z(t) = eit, t E [0, 7/2] Then Edz = (TT / 2 e itie it at C |71 / 2 = it 0 = 27/2 21 NOTE: The result of the integration is path-dependent.Examples We want to compute the integral zdz where C is the . line between z1 = 1 and z2 = i z(t) = 1 + t(i - 1), te [0, 1] 22 Then J zdz = 1 (1+1(i-1)(1-1)at z1 = (2 - 1)(t+ 2 (2 - 1))| = (i-1)1+2 2 = - 1 . arc of unit circle between z1 and z2 = i z(t) = eit, t E [0, 7/2] Then 2it /2" = -1 21 NOTE: The result of the integration is the same for the two contours. Is it that the integral is path-independent and if so, why? Line integral in the complex plane Cauchy's Integral Theorem Cauchy's Integral Formula Derivatives of analytic functions Integral of analytic functions: evaluation method 2 Calculus theorem * Consider a complex function f(z) which is analytic in a simply connected domain D. Then There exists a function F(z), analytic in D, such that F' (z) = f(z) The line integral of f(z) along any path C C D that starts at z1 and ends at 22 is constant (i.e., independent of the path) f ( z ) dz = F (22) - F(z1) Example: zdz = 23/2 - 21/2 = -1, if z1 = 1 and z2 = i. NOTE: Allows to compute complex integrals using the same techniques as real integrals.Q1. (20 points) 3%. %52dz, C is the ellipse 4:132 + 43/2 = 1 (Hint: (mg2h? + (9221102 2 1 represents the ellipse that centers at (h,w) with horizontal radius of a and vertical radius of b.) Q2. (20 points) Integrate the following complex function by both \"evaluation method 1\" and \"evaluation method 2\" in lecture notes. If \"evaluation method 2\" cannot be used, state the reason. f0 Re(z2)dz, C is the shortest path from 1 to 2 + 1'. Q3. (10 points) Integrate counterclockwise around the unit circle. dz ZS f0 W