Attached are some extra information that would be helpful, please let me know if you need more info

just the part b sorry

Exclude part a

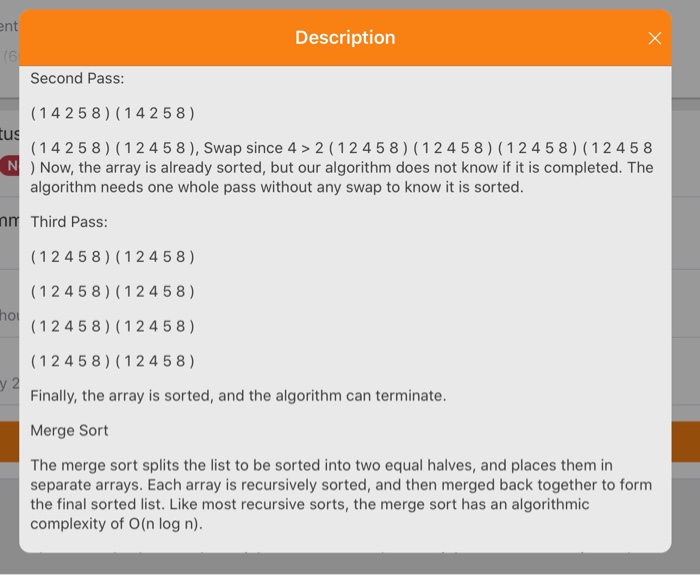
nt Description (6 a. Describe a method for finding both the maximum and minimum of n numbers using fewer than 3n/2 comparisons. us b. Suppose each row of an nxn array A only consists of 1's and O's such that, in any row i of A, all the 1's come before any O's. Assuming A is already in memory, m describe a method running in O(nlog n) time for counting the number of 1's in A. Here is a simple example of bubble sort. Let us take the array of numbers "5 14 2 8", and sort the array from lowest number to o greatest number using bubble sort algorithm. First Pass: 12 (514 28)(154 28), Here, algorithm compares the first two elements, and swaps them. (154 28) (14 5 2 8), Swap since 5 > 4 ( 145 2 8) (14 258), Swap since 5 > 2 (14 258) (14258), Now, since these elements are already in order (8 > 5), algorithm does not swap them. Second Pass: (14258) (14258) ent Description (6 Second Pass: (14258) (14 2 58) tus (14258) (12 4 58), Swap since 4 > 2 ( 12 4 58) (124 58) (1 2 4 5 8) (124 5 8 N)Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted. nm Third Pass: (124 58) (124 58) (12458) (12 4 58) ho (124 58) (12 4 5 8) (12458) (124 58) y 2 Finally, the array is sorted, and the algorithm can terminate. Merge Sort The merge sort splits the list to be sorted into two equal halves, and places them in separate arrays. Each array is recursively sorted, and then merged back together to form the final sorted list. Like most recursive sorts, the merge sort has an algorithmic complexity of O(n log n). nment Description part (6 complexity of O(n log n). Elementary implementations of the merge sort make use of three arrays - one for each status half of the data set and one to store the sorted list in. The below algorithm merges the arrays in-place, so only two arrays are required. There are non-recursive versions of the merge sort, but they don't yield any significant performance enhancement over the recursive algorithm on most machines. comm Pros: Marginally faster than the heap sort for larger sets. (0) Cons: At least twice the memory requirements of the other sorts; recursive. ing - an ho Merge Sort Efficiency The merge sort is slightly faster than the heap sort (to be covered) for larger sets, but it requires twice the memory of the heap sort because of the second array. This additional memory requirement makes it unattractive for most purposes - the quick sort is a better nuary 2 choice most of the time and the heap sort is a better choice for very large sets. Like the quick sort, the merge sort is recursive which can make it a bad choice for applications that run on machines with limited memory. Source Code Below is the basic merge sort algorithm. void mergeSort(int numbers[], int temp[], int array_size) { Description void mergeSort(int numbers[], int temp[], int array_size) { m_sort(numbers, temp, 0, array_size - 1); } void m_sort(int numbers[], int temp[], int left, int right) { int mid; if (right > left) { mid = (right + left) / 2; m_sort(numbers, temp, left, mid); m_sort(numbers, temp, mid+1, right); merge (numbers, temp, left, mid+1, right); } void merge(int numbers[], int temp[], int left, int mid, int right) { int i, left_end, num_elements, tmp_pos3B ent Description (6 int i, left_end, num_elements, tmp_pos; left_end = mid - 1; tus tmp_pos = left; num_elements = right - left + 1; nm while (left