Attached I have a question with the answer but I have a follow up question to the answer.

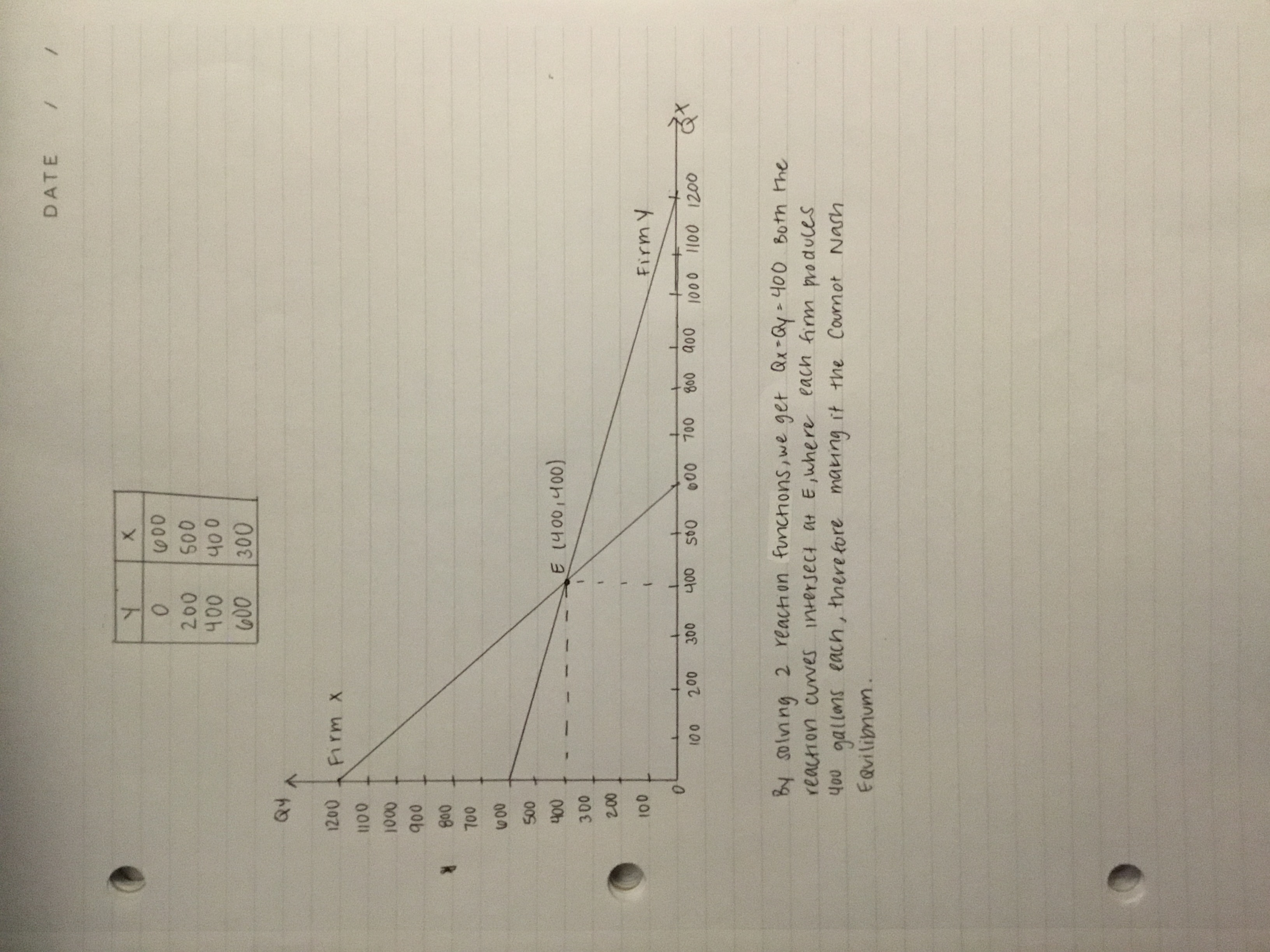
CHALLENGES 14. The French economist Antoine Cournot devel Based on this demand schedule, calculate the oped an interesting model of competition in demand schedule that Firm X would face if it ever, suspected Firm Y was going to going to produce 0, 200, on t an oligopoly that now bears his name. In a P oligopoly, all of the firms know that 400, or 600 gallons of spring water. Then, figure the total output from all firms will determine out the profit-maximizing amount of spring water for Firm X to produce in response. Fill in the price (based on the downward-sloping the table. market demand curve ) , but they make inde - pendent and simultaneous decisions about how much output to produce . Cournot developed . . . then Firm X should If Firm Y produces ... produce . .. this model after observing how a spring water duopoly (two firms) behaved. So let's look at a 0 gal duopoly example. 200 gal For each firm to decide how much to pro- 400 gal duce, it must make a guess about how much the other firm is going to produce. Also, the firms 600 gal basically assume that once the other firm has decided how much to produce, it can't really change its decision. What you have just constructed is what Here's an example. Suppose the market economists would call Firm X's reaction function. demand curve for gallons of fresh spring water Even though Firm X thought about the differ- looks like the one in the next table and, to keep ent choices Firm Y could make, Firm Y is not things simple, the marginal cost of spring water actually going to choose just any random level of output. In fact, Firm Y has its own reaction is zero. If Firm X believes that Firm Y is going to function, where it considers how best to respond produce 100 gallons of spring water, for example, to what it thinks Firm X is doing. Because both then Firm X knows that if it produces 0 gallons, firms have the same zero marginal cost, the two the price will be $2.75; if it produces 100 gal- reaction functions are symmetrical. (Thus, Firm lons, the price will be $2.50, and so on. Basically, Y's reaction function looks the same, only with Firm X will face its own demand curve where "X" and "Y" switched.) all of the quantities are lower by 100. Graph the two reaction functions. Do you notice any points that stand out? Describe why Market Demand this point represents an equilibrium for both firms. Price Quantity Demanded (gal) 15. The following diagram shows the monthly demand for hot dogs in a large city. The mar- $3.00 0 ginal cost (and average cost) is a constant $2 per $2.75 hot dog. 100 $2.50 200 Price $2.25 300 $2.00 400 $1.75 500 $1.50 600 $4 $1.25 700 $1.00 800 Demand $0.75 900 80 100 Quantity $0.50 (thousands 1,000 The Market for Hot DogsDATE y X O 600 200 500 400 40 0 600 300 Q4 ~ 1200 Firm x 1100 1000 900 800 700 600 500 400 E (400, 400) 300 200 100 Firm y 100 200 300 400 500 600 700 800 900 1000 1100 1200 By solving 2 reaction functions, we get Qx- Qy = 400 Both the reaction curves intersect at E, where each firm produces 400 gallons each , therefore making it the Cournot Nash EQuilibrium .