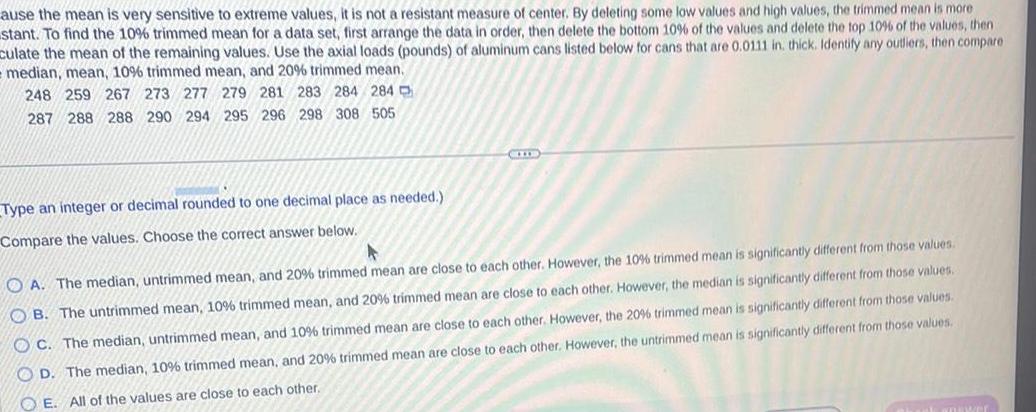
ause the mean is very sensitive to extreme values, it is not a resistant measure of center. By deleting some low values and high values, the trimmed mean is more stant. To find the 10% trimmed mean for a data set, first arrange the data in order, then delete the bottom 10% of the values and delete the top 10% of the values, then culate the mean of the remaining values. Use the axial loads (pounds) of aluminum cans listed below for cans that are 0.0111 in. thick. Identify any outliers, then compare median, mean, 10% trimmed mean, and 20% trimmed mean. 248 259 267 273 277 279 281 283 284 284 287 288 288 290 294 295 296 298 308 505 Type an integer or decimal rounded to one decimal place as needed.) Compare the values. Choose the correct answer below. OA. The median, untrimmed mean, and 20% trimmed mean are close to each other. However, the 10% trimmed mean is significantly different from those values. OB. The untrimmed mean, 10% trimmed mean, and 20% trimmed mean are close to each other. However, the median is significantly different from those values. OC. The median, untrimmed mean, and 10% trimmed mean are close to each other. However, the 20% trimmed mean is significantly different from those values. OD. The median, 10% trimmed mean, and 20% trimmed mean are close to each other. However, the untrimmed mean is significantly different from those values. OE. All of the values are close to each other.