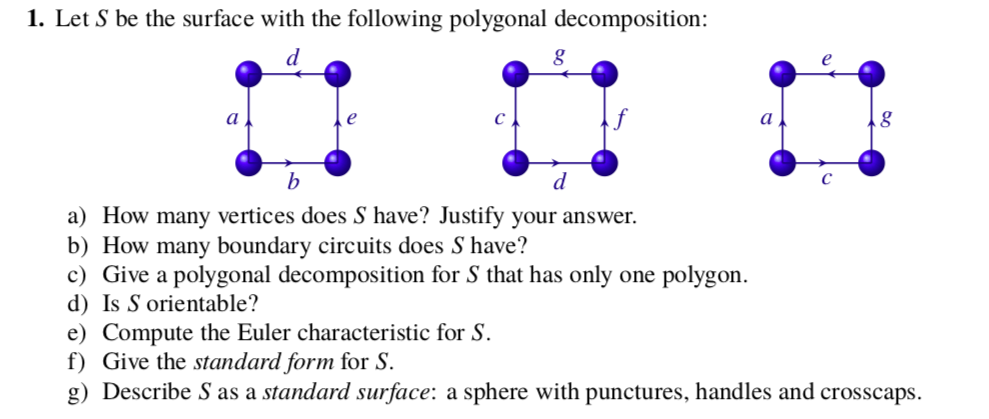
b) Does this still hold when we allow G to have loops or parallel edges? Provide a proof or a counterexample. 5. Let G be a connected graph. In lecture, we defined an Euler circuit in G as a circuit in G that goes through every edge exactly once. Similarly, we may define an Euler path in G as a path in G that goes through every edge exactly once. a) Give an example of a graph which has an Euler path, but which has no Euler circuit. b) Prove that G has an Euler path but no Euler circuit if and only if exactly two vertices in G have odd degree. You may use any result we proved in lecture. c) For which n does the complete graph K, have an Euler path but no Euler circuit?1. Let S be the surface with the following polygonal decomposition: d 3 e b d C a) How many vertices does S have? Justify your answer. b) How many boundary circuits does S have? c) Give a polygonal decomposition for S that has only one polygon. d) Is S orientable'? e) Compute the Euler characteristic for S. f) Give the standardform for S. g) Describe S as a standard surface: a sphere with punctures, handles and crosscaps. 2. For each of the following properties, give an example of a connected surface with that property or explain why such a surface does not exist. If the surface does exist then draw its standard polygonal decomposition. a) An oriented surface with Euler characteristic 3. b) A non-oriented closed surface with Euler characteristic 4. 3. Give a complete list of all the (connected) oriented surfaces with Euler characteristic -5, written in standard form. 4. Let G be a (nite) graph without loops or parallel edges, and with at least two vertices. a) Prove that G contains a pair of distinct vertices of the same degree