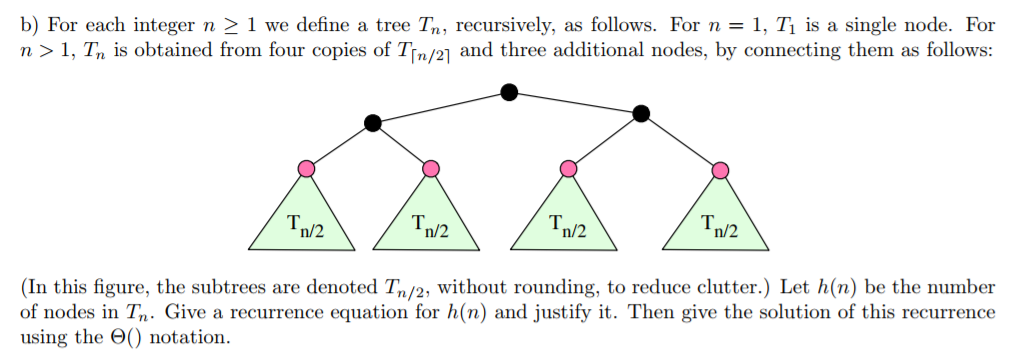
b) For each integer n 2 1 we define a tree Tn, recursively, as follows. For n 1, Ti is a single node. For n > 1, Tn is obtained from four copies of Tn/21 and three additional nodes, by connecting them as follows: T. n/2 n/2 n/2 n/2 (In this figure, the subtrees are denoted Tn/2, without rounding, to reduce clutter.) Let h(n) be the number of nodes in T. Give a recurrence equation for h(n) and justify it. Then give the solution of this recurrence using the () notation