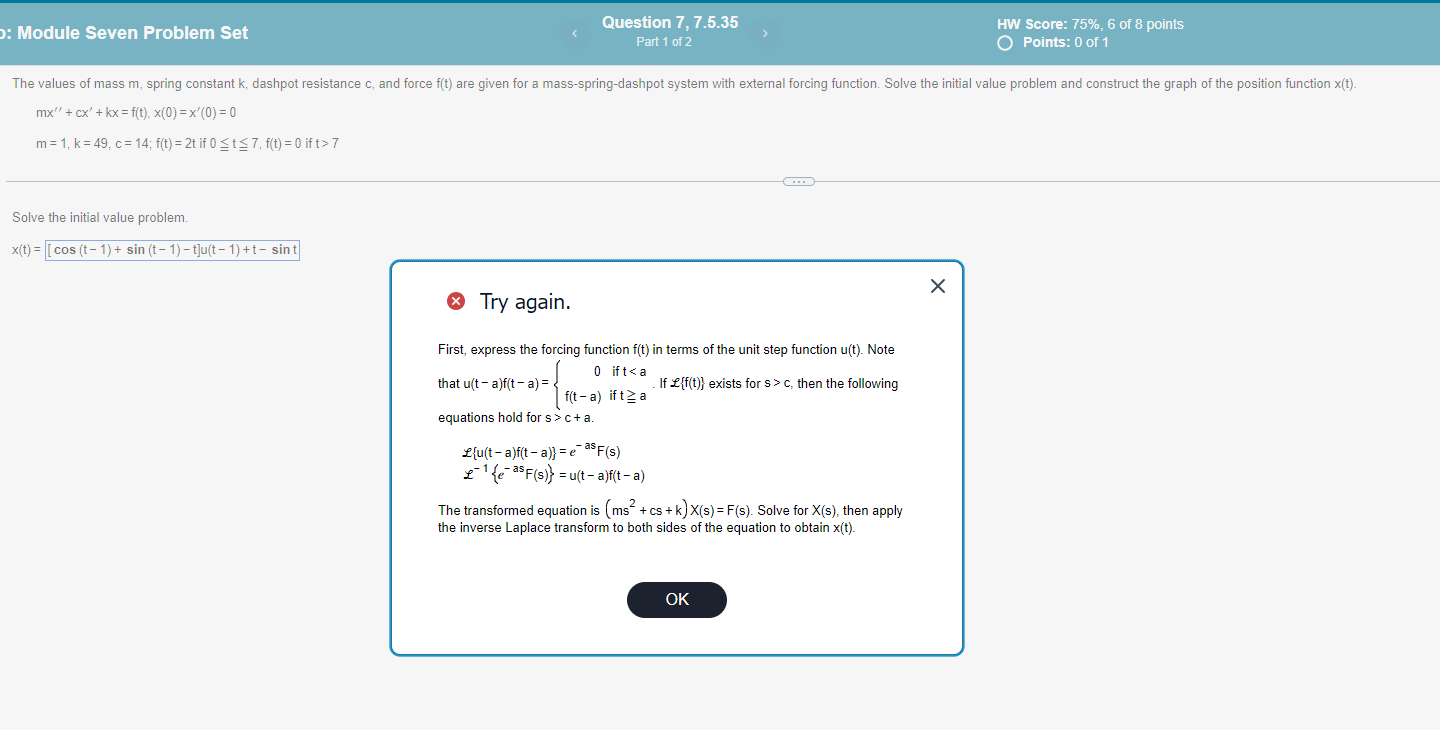
b: Module Seven Problem Set Question 7, 7.5.35 HW Score: 75%, 6 of 8 points Part 1 of 2 O Points: 0 of 1 Save The values of mass m, spring constant k, dashpot resistance c, and force f(t) are given for a mass-spring-dashpot system with external forcing function. Solve the initial value problem and construct the graph of the position function x(t). mx" + cx' + kx = f(t), x(0) = x'(0) = 0 m = 1, k = 49, c= 14; f(t) = 2t if 0 ty 7, f(t) = 0 ift> 7 Solve the initial value problem. x(1) =: Module Seven Problem Set Question 7, 7.5.35 HW Score: 75%, 6 of 8 points Part 1 of 2 O Points: 0 of 1 The values of mass m, spring constant k, dashpot resistance c, and force f(t) are given for a mass-spring-dashpot system with external forcing function. Solve the initial value problem and construct the graph of the position function x(t). mx" + cx' + kx = f(t), x(0) = x'(0) = 0 m = 1, k = 49, c= 14; f(t) = 2t if 0 t 7, f(t) = 0 ift> 7 Solve the initial value problem. x(1) = [ cos (t- 1) + sin (t- 1) -tju(t - 1) +t- sint X Try again. First, express the forcing function f(t) in terms of the unit step function u(t). Note 0 ift c, then the following equations hold for s > c ta. flu(t - a)f(t - a)} = e" asF(s) 2 1 {e- asF(s)) = u(t - a)f(t -a) The transformed equation is (ms + cs + k) X(s) = F(s). Solve for X(s), then apply the inverse Laplace transform to both sides of the equation to obtain x(t). OKa ) miven m= 1, K = 49 , c 0 . dem *" + 14x' + yox = fit - - Taking Ly on both sides, 7 5" x(s) - 5 x 20) -34(0) + 14/5 x 105) - 210)J + 4957 = fundt 5 ) PEER S' X (57 0 + 145 x (3 , + 49 * 4 , = (o ) de 1 2 + AMS + 49 = 2 1 -75 - 75 = 21-7 + + 3 2 = - 20 - 75 2 - 2e -75 s+7 ) + S 7 7 Xcy . #(5 +7 ) 2 = ) X