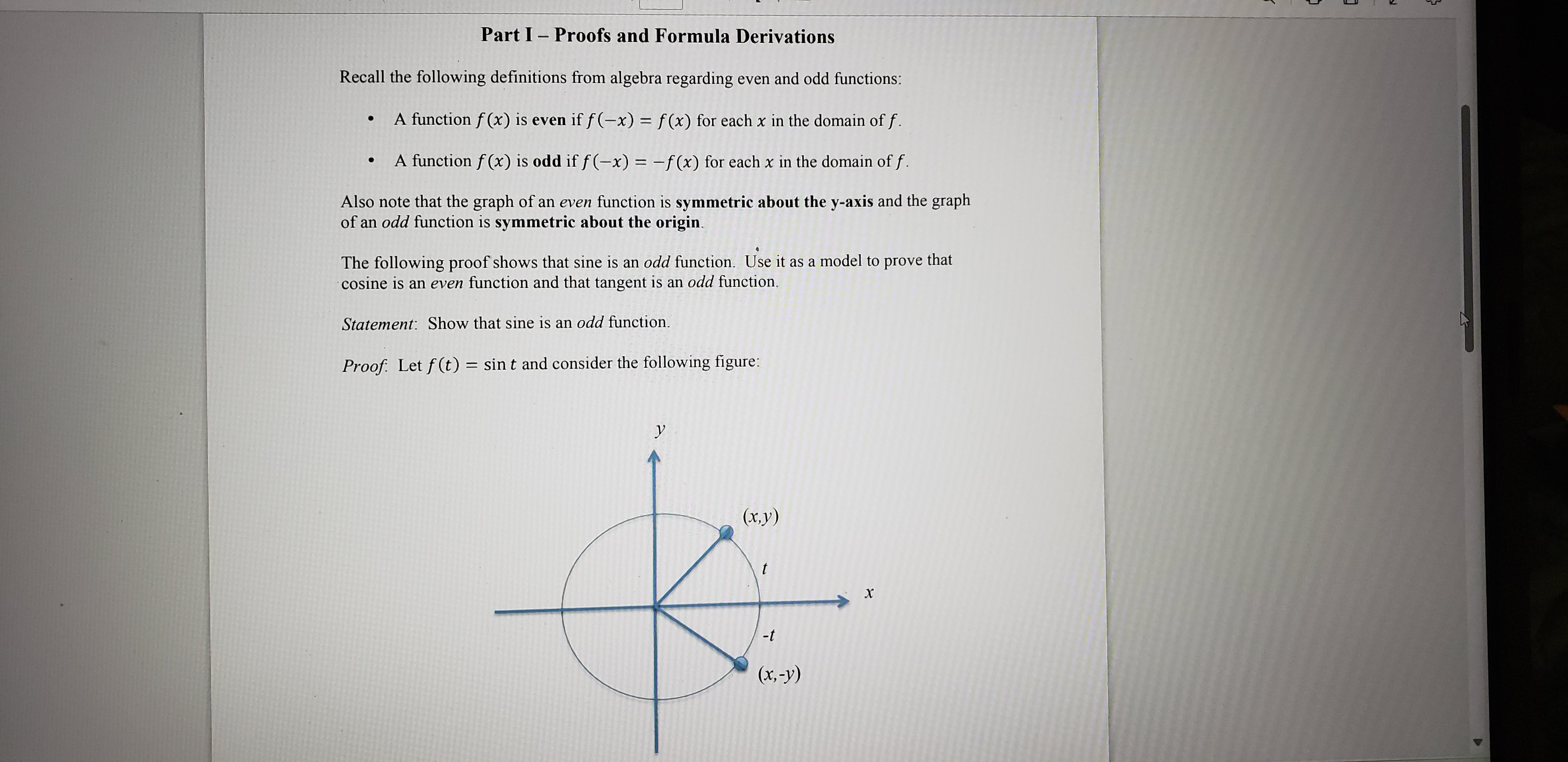
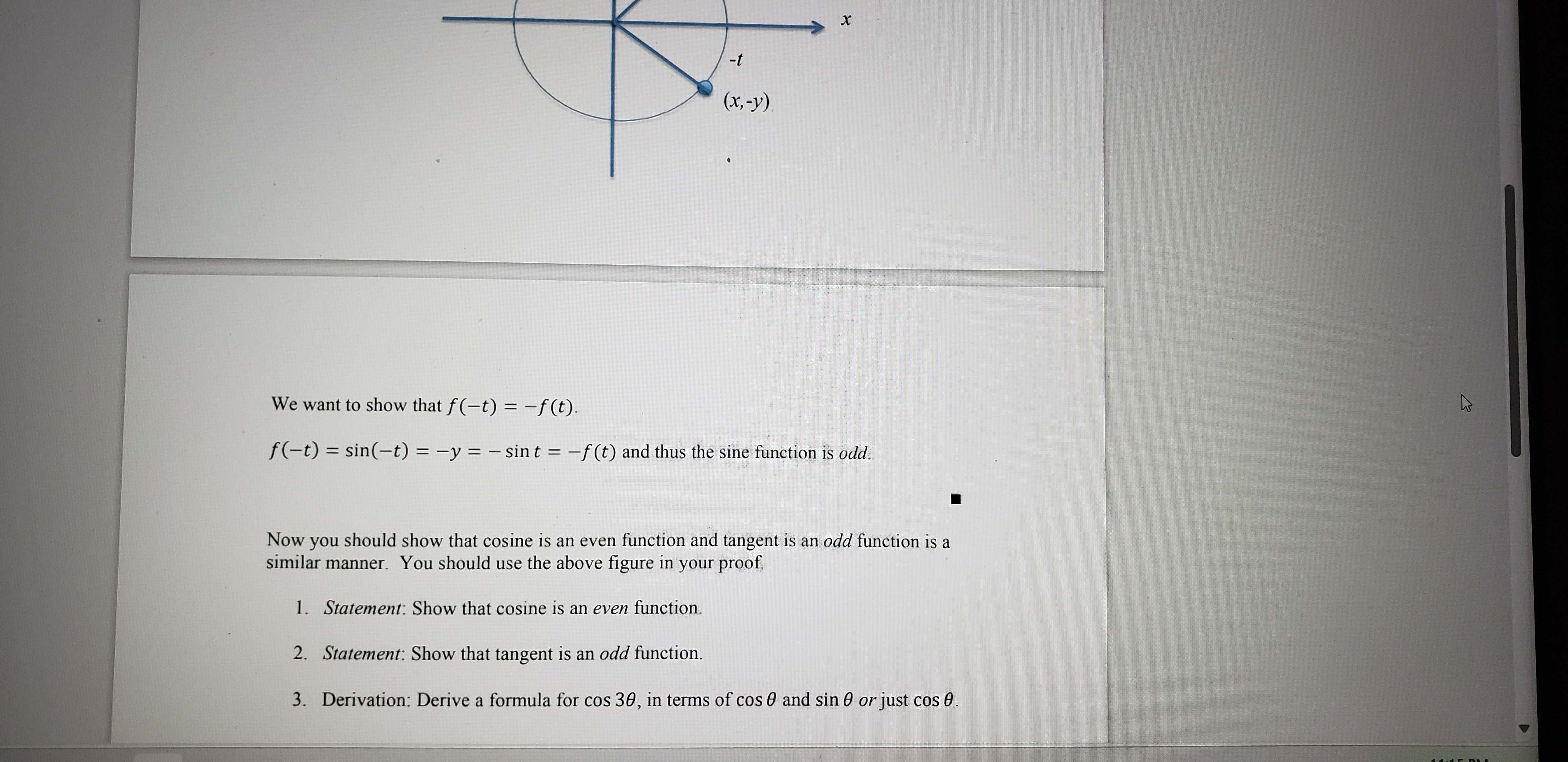
. - B Part I - Proofs and Formula Derivations >call tiw follov;ring definitions from algebra regarding even and odd funco;ns: * A function f(x) is even if f(x) = f(x) for each x in the domain of f. e A function f(x) is odd if f(x) = f(x) for each x in the domain of f. Also note that the graph of an even function is symmetric about the y-axis and the graph of an odd function is symmetric about the origin. The following proof shows that sine is an odd function. Use it as a model to prove that \"cosine is an even function and that tangent is an odd function. Statement: Show that sine is an odd function. Proof: Let f(t) = sint and consider the following figure: We want to show that f(t) = f(t). f(=t) =sin(t) = y = sint = f(t) and thus the sine function is odd. n 'Now you should show that cosine is an even function and tangent is an odd function is a 'similar manner. You should use the above figure in your proof. i Statement: Show that cosine is an even function. ement: Show that tangent is an odd function. Part II - Conceptual Questions 1. True or False? Explain your answer. Because sin(-t) = - sin t, it can be said that the sine of a negative angle is a negative number. Part III - Application 1. Answer the following questions. Be sure to show your work. A weight is attached to a spring suspended vertically from a ceiling. When a driving force is applied to the system, the weight moves vertically from its equilibrium position, and this motion is modeled by 3 sin 2t + = cos 2t where y is the distance from equilibrium (in feet) and t is the time (in seconds). a. Use the identity a . sinBO + b . cos BO = va2 + b2 . sin(Bt + C) where C = arctan ( ) , a > o, to write the model in the form y = va2 + b2 . sin(Bt + C). b. State the amplitude of the oscillations of the weight. c. Find the frequency of the oscillations of the weight