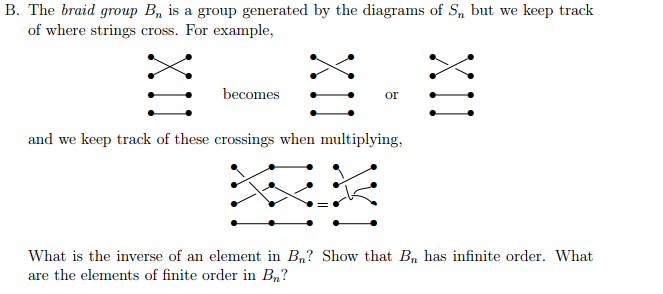
B. The braid group Bn is a group generated by the diagrams of Sn but we keep track of where strings cross. For example, Co C) Co becomes or Co and we keep track of these crossings when multiplying, C) C) Co 0 O What is the inverse of an element in Bn Show that Bn has infinite order. What are the elements of finite order in Bn B. The braid group Bn is a group generated by the diagrams of Sn but we keep track of where strings cross. For example, Co C) Co becomes or Co and we keep track of these crossings when multiplying, C) C) Co 0 O What is the inverse of an element in Bn Show that Bn has infinite order. What are the elements of finite order in Bn