Base code:
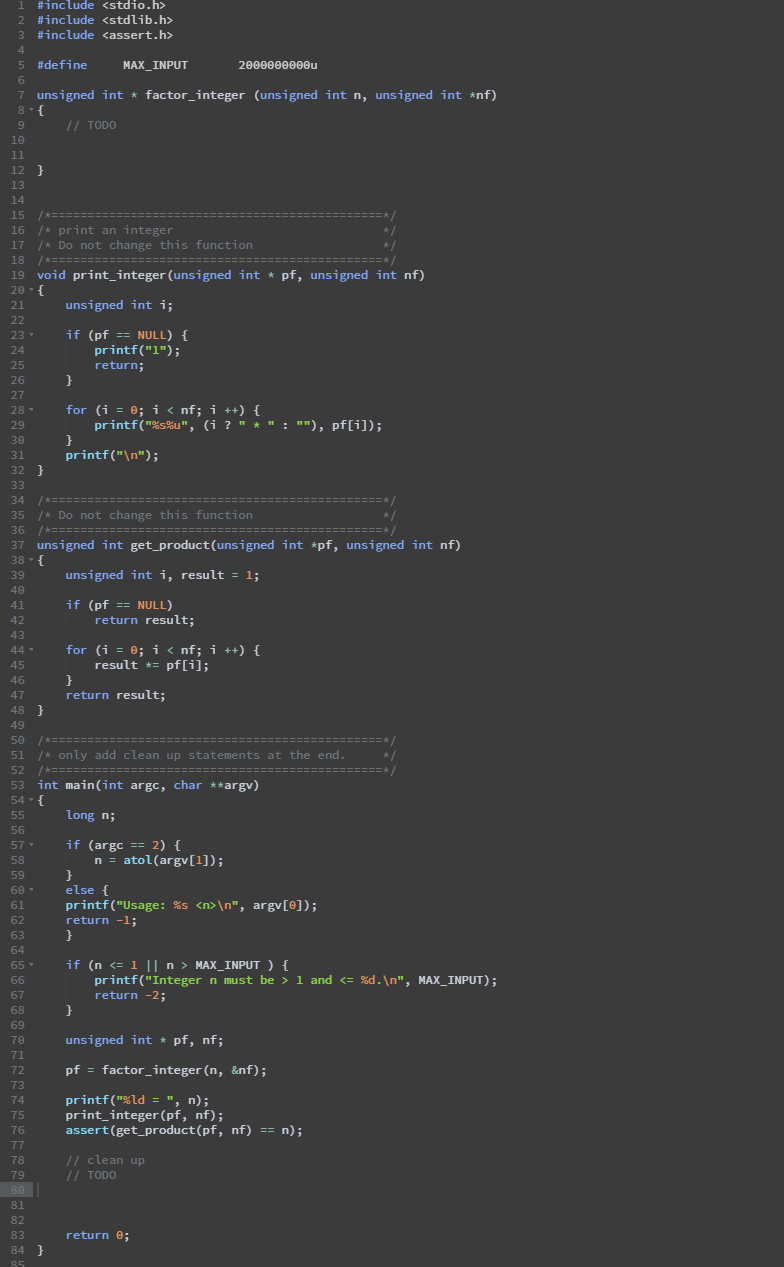
Exercise 1. (30 points) Prime factorization. Finding prime factors for large integers is a difficult problem. However, doing so for small integers is not hard. In this assignment, you will implement a function factor integer () that finds all prime factors of a given an unsigned integer n>1. The prototype of the function is: unsigned int * factor_integer (unsigned int n, unsigned int *nf); factor_integer() must find all prime factors of n and store them in a dynamically allocated array in non-decreasing order. It then returns the starting address of the array. The number of prime factors in the array is stored in an integer pointed to by nf. The product of all elements in the factor array should be exactly n. factor_integer() should return NULL if n is 0 or 1. For example, if n is 20, the returned array has three elements: 2, 2, 5, and *nf is 3. If n is 7, the returned array has one element: 7, and *nf is 1. Here are some sample sessions of running the program. You can use a calculator to check that the number is indeed the product of all reported prime factors. $./factor 64 64=2 * 2 * 2 * 2 * 2 * 2 $./factor 192 192=2 * 2 * 2 * 2 * 2 * 2 * 3 $./factor 123456789 123456789=3 * 3 * 3607 * 3803 $./factor 1234567890 1234567890=2 * 3 * 3 * 5 * 3607 * 3803 ./factor 1999999973 1999999973=1999999973 ./factor 2000000000 2000OONNNN=? * 2 * 2 * 2 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 1 #include
2 #include 3 #include 4 5 #define MAX_INPUT 2000000000u 6 6 7 unsigned int * factor_integer (unsigned int n, unsigned int *nf) 8-{ 9 // TODO 10 11 12} 13 14 15 /*======: 16 /* print an integer */ 17 /* Do not change this function 18 /*============================ */ 19 void print_integer (unsigned int * pf, unsigned int nf) 20 - { 24 * 21 unsigned int i; 22 23 - if (pf == NULL) { printf("1"); 25 return; 26 } 27 28 - for (i = 0; i ", argv[@]); 62 return -1; 63 } 64 65 if (n MAX_INPUT ) { 66 printf("Integer n must be > 1 and 1. The prototype of the function is: unsigned int * factor_integer (unsigned int n, unsigned int *nf); factor_integer() must find all prime factors of n and store them in a dynamically allocated array in non-decreasing order. It then returns the starting address of the array. The number of prime factors in the array is stored in an integer pointed to by nf. The product of all elements in the factor array should be exactly n. factor_integer() should return NULL if n is 0 or 1. For example, if n is 20, the returned array has three elements: 2, 2, 5, and *nf is 3. If n is 7, the returned array has one element: 7, and *nf is 1. Here are some sample sessions of running the program. You can use a calculator to check that the number is indeed the product of all reported prime factors. $./factor 64 64=2 * 2 * 2 * 2 * 2 * 2 $./factor 192 192=2 * 2 * 2 * 2 * 2 * 2 * 3 $./factor 123456789 123456789=3 * 3 * 3607 * 3803 $./factor 1234567890 1234567890=2 * 3 * 3 * 5 * 3607 * 3803 ./factor 1999999973 1999999973=1999999973 ./factor 2000000000 2000OONNNN=? * 2 * 2 * 2 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 1 #include 2 #include 3 #include 4 5 #define MAX_INPUT 2000000000u 6 6 7 unsigned int * factor_integer (unsigned int n, unsigned int *nf) 8-{ 9 // TODO 10 11 12} 13 14 15 /*======: 16 /* print an integer */ 17 /* Do not change this function 18 /*============================ */ 19 void print_integer (unsigned int * pf, unsigned int nf) 20 - { 24 * 21 unsigned int i; 22 23 - if (pf == NULL) { printf("1"); 25 return; 26 } 27 28 - for (i = 0; i ", argv[@]); 62 return -1; 63 } 64 65 if (n MAX_INPUT ) { 66 printf("Integer n must be > 1 and
