Baseball A (Square) Baseball Diamond Has Sides That Are 90 Feet Long (See Figure). A Player Running From Second Base To Third Base At A Speed Of 25 Feet Per Second Is 21 Feet From Third Base. At What Rate (In Ft/Sec) Is The Player's Distance From Home Plate Changing? (Round Your Answer To Two Decimal Places.) M/Sec DETAILS LARAPCALC10 2.6.044 MY NOTES

 

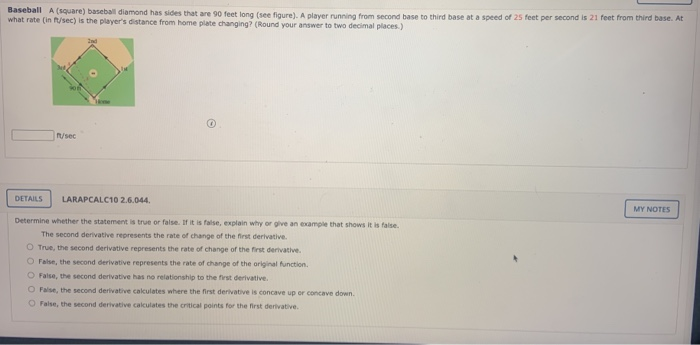
Baseball A (square) baseball diamond has sides that are 90 feet long (see figure). A player running from second base to third base at a speed of 25 feet per second is 21 feet from third base. At what rate (in ft/sec) is the player's distance from home plate changing? (Round your answer to two decimal places.) /sec DETAILS LARAPCALC10 2.6.044. Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. The second derivative represents the rate of change of the first derivative. O True, the second derivative represents the rate of change of the first derivative. O False, the second derivative represents the rate of change of the original function. O False, the second derivative has no relationship to the first derivative. O False, the second derivative calculates where the first derivative is concave up or concave down. O False, the second derivative calculates the critical points for the first derivative. MY NOTES