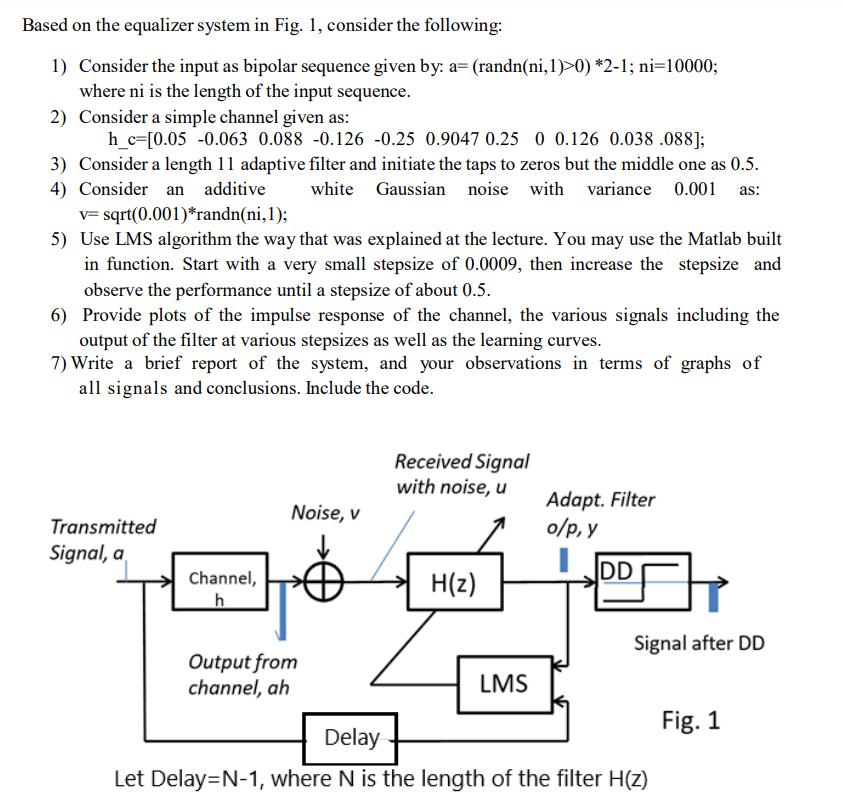
• 
  
  • 
    
    • 
      
      • 
        
        • 
          
          • 
            
            • 
              
              • 
                
                • 
                  

Based on the equalizer system in Fig. 1, consider the following: 1) Consider the input as bipolar sequence given by: a= (randn(ni,1)>0) *2-1; ni=10000; where ni is the length of the input sequence. 2) Consider a simple channel given as: h_c [0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 .088]; 3) Consider a length 11 adaptive filter and initiate the taps to zeros but the middle one as 0.5. 4) Consider an additive white Gaussian noise with variance 0.001 as: v= sqrt(0.001)*randn(ni, 1); 5) Use LMS algorithm the way that was explained at the lecture. You may use the Matlab built in function. Start with a very small stepsize of 0.0009, then increase the stepsize and observe the performance until a stepsize of about 0.5. 6) Provide plots of the impulse response of the channel, the various signals including the output of the filter at various stepsizes as well as the learning curves. 7) Write a brief report of the system, and your observations in terms of graphs of all signals and conclusions. Include the code. Transmitted Signal, a Channel, h Noise, v Output from channel, ah Received Signal with noise, u H(z) LMS Adapt. Filter o/p, y DD Signal after DD Delay Let Delay=N-1, where N is the length of the filter H(z) Fig. 1