Based on the following example, I need help proving exercise 5. Thank you.

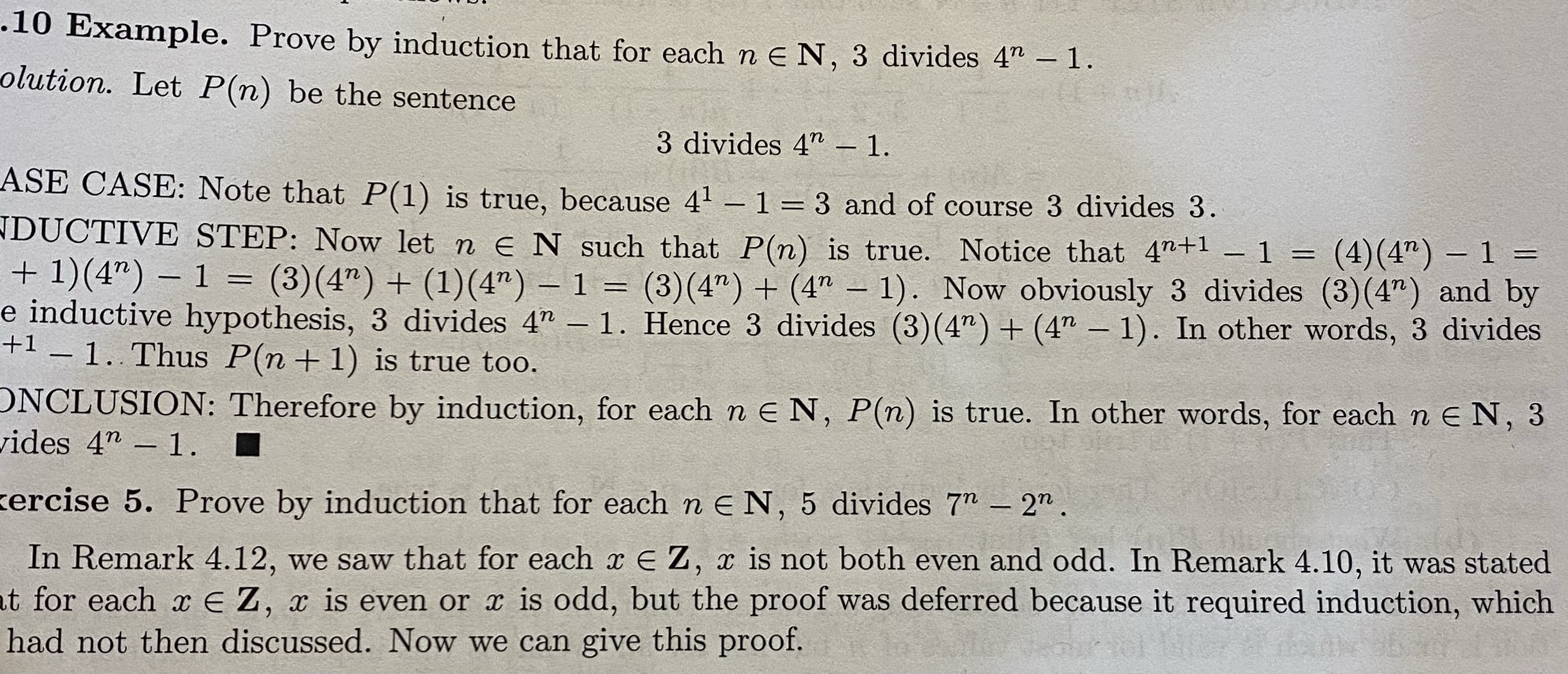
10 Example. Prove by induction that for each n E N, 3 divides 4" - 1. olution. Let P(n) be the sentence 3 divides 4" - 1. ASE CASE: Note that P(1) is true, because 41 - 1 = 3 and of course 3 divides 3. DUCTIVE STEP: Now let n E N such that P(n) is true. Notice that 4nti - 1 = (4)(4n) - 1 = + 1)(40) - 1 = (3)(4n) + (1)(47) - 1 = (3)(4") + (4" -1). Now obviously 3 divides (3) (4" ) and by e inductive hypothesis, 3 divides 4" - 1. Hence 3 divides (3) (4") + (4" - 1). In other words, 3 divides +1 - 1. Thus P(n + 1) is true too. ONCLUSION: Therefore by induction, for each n E N, P(n) is true. In other words, for each n E N, 3 ides 4" - 1. cercise 5. Prove by induction that for each n E N, 5 divides 7n - 2n. In Remark 4.12, we saw that for each x E Z, x is not both even and odd. In Remark 4.10, it was stated t for each x E Z, x is even or x is odd, but the proof was deferred because it required induction, which had not then discussed. Now we can give this proof