Based on the training accuracy, do you conclude that the data are linearly separable? Why or why not?

2.2 Which feature most increases the likelihood that the class is 'Android' and which feature most increases the likelihood that the class is 'iPhone'?

2.3 Compare the initial training/test accuracies to the training/test accuracies after averaging. What happens? Why do you think averaging the weights from different iterations has this effect?

from sklearn.linear_model import SGDClassifier

from sklearn.metrics import accuracy_score, precision_score

classifier = SGDClassifier(loss='perceptron', max_iter=1000, tol=1.0e-12, random_state=123, eta0=100)

classifier.fit(X_train, Y_train)

print("Number of SGD iterations: %d" % classifier.n_iter_)

print("Training accuracy: %0.6f" % accuracy_score(Y_train, classifier.predict(X_train)))

print("Testing accuracy: %0.6f" % accuracy_score(Y_test, classifier.predict(X_test)))

print("\nFeature weights:")

args = np.argsort(classifier.coef_[0])

for a in args:

print(" %s: %0.4f" % (feature_names[a], classifier.coef_[0][a]))
 

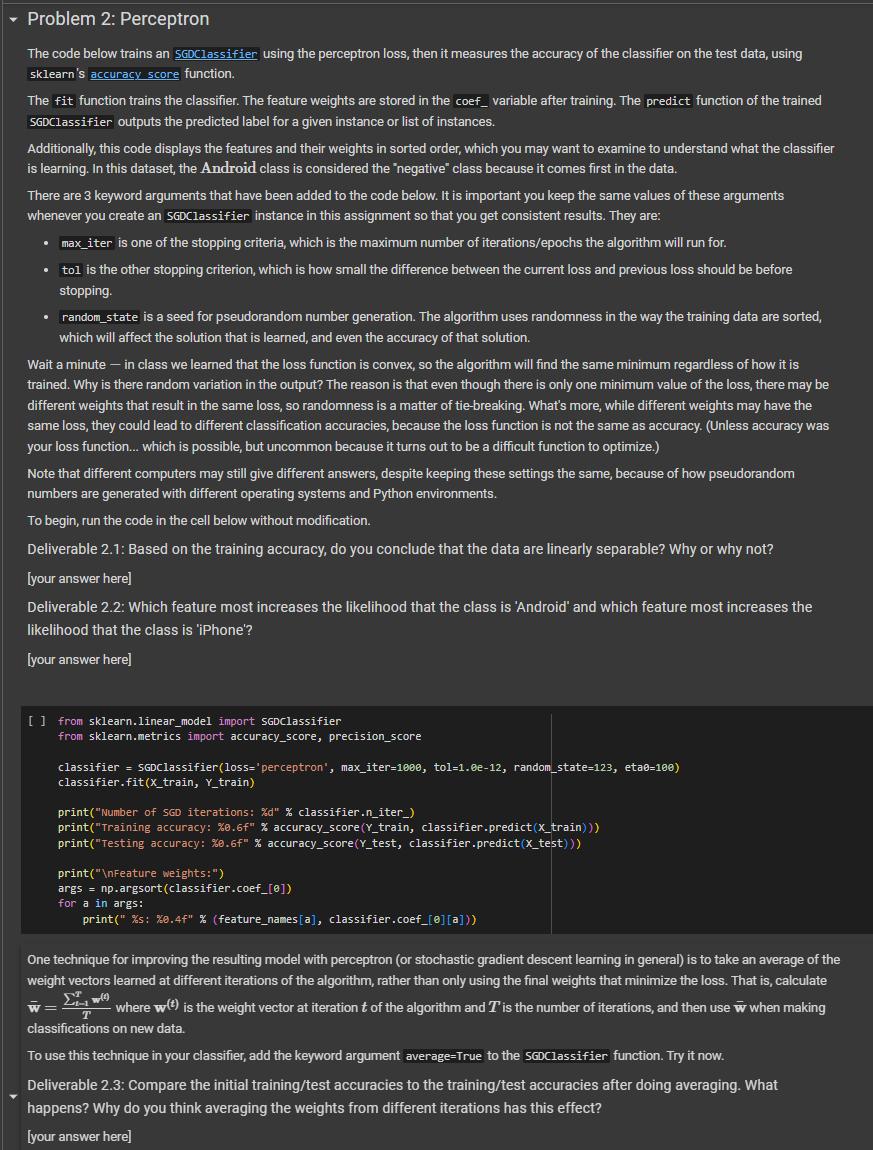
Problem 2: Perceptron The code below trains an SGDClassifier using the perceptron loss, then it measures the accuracy of the classifier on the test data, using sklearn's accuracy score function. The fit function trains the classifier. The feature weights are stored in the coef_variable after training. The predict function of the trained SGDClassifier outputs the predicted label for a given instance or list of instances. Additionally, this code displays the features and their weights in sorted order, which you may want to examine to understand what the classifier is learning. In this dataset, the Android class is considered the "negative" class because it comes first in the data. There are 3 keyword arguments that have been added to the code below. It is important you keep the same values of these arguments whenever you create an SGDClassifier instance in this assignment so that you get consistent results. They are: max_iter is one of the stopping criteria, which is the maximum number of iterations/epochs the algorithm will run for. tol is the other stopping criterion, which is how small the difference between the current loss and previous loss should be before stopping. random_state is a seed for pseudorandom number generation. The algorithm uses randomness in the way the training data are sorted, which will affect the solution that is learned, and even the accuracy of that solution. Wait a minute - in class we learned that the loss function is convex, so the algorithm will find the same minimum regardless of how it is trained. Why is there random variation in the output? The reason is that even though there is only one minimum value of the loss, there may be different weights that result in the same loss, so randomness is a matter of tie-breaking. What's more, while different weights may have the same loss, they could lead to different classification accuracies, because the loss function is not the same as accuracy. (Unless accuracy was your loss function... which is possible, but uncommon because it turns out to be a difficult function to optimize.) Note that different computers may still give different answers, despite keeping these settings the same, because of how pseudorandom numbers are generated with different operating systems and Python environments. To begin, run the code in the cell below without modification. Deliverable 2.1: Based on the training accuracy, do you conclude that the data are linearly separable? Why or why not? [your answer here] Deliverable 2.2: Which feature most increases the likelihood that the class is 'Android' and which feature most increases the likelihood that the class is 'iPhone'? [your answer here] [ ] from sklearn.linear_model import SGDClassifier from sklearn.metrics import accuracy_score, precision_score classifier = SGDClassifier (loss=' perceptron', max_iter=1000, tol=1.8e-12, random_state=123, eta0=100) classifier.fit(x_train, Y_train) print("Number of SGD iterations: %d" % classifier.n_iter_) print("Training accuracy: %0.6f" % accuracy_score (Y_train, classifier.predict(x_train))) print("Testing accuracy: %0.6f" % accuracy_score (Y_test, classifier.predict(X_test))) print(" Feature weights:") args = np.argsort (classifier.coef_[0]) for a in args: print("%s: %0.4f" % (feature_names[a], classifier.coef [e] [a])) One technique for improving the resulting model with perceptron (or stochastic gradient descent learning in general) is to take an average of the weight vectors learned at different iterations of the algorithm, rather than only using the final weights that minimize the loss. That is, calculate 1-1 T W= where w(t) is the weight vector at iteration t of the algorithm and T is the number of iterations, and then use w when making classifications on new data. To use this technique in your classifier, add the keyword argument average=True to the SGDClassifier function. Try it now. Deliverable 2.3: Compare the initial training/test accuracies to the training/test accuracies after doing averaging. What happens? Why do you think averaging the weights from different iterations has this effect? [your answer here]