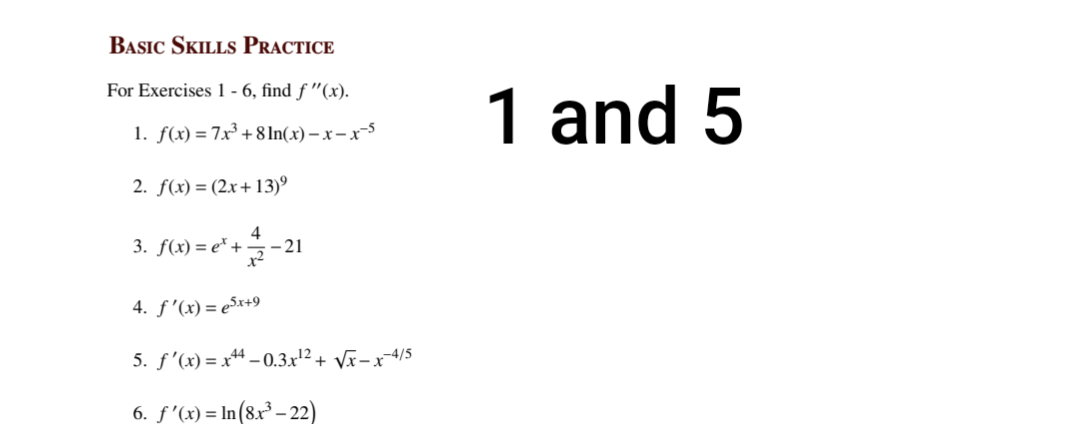
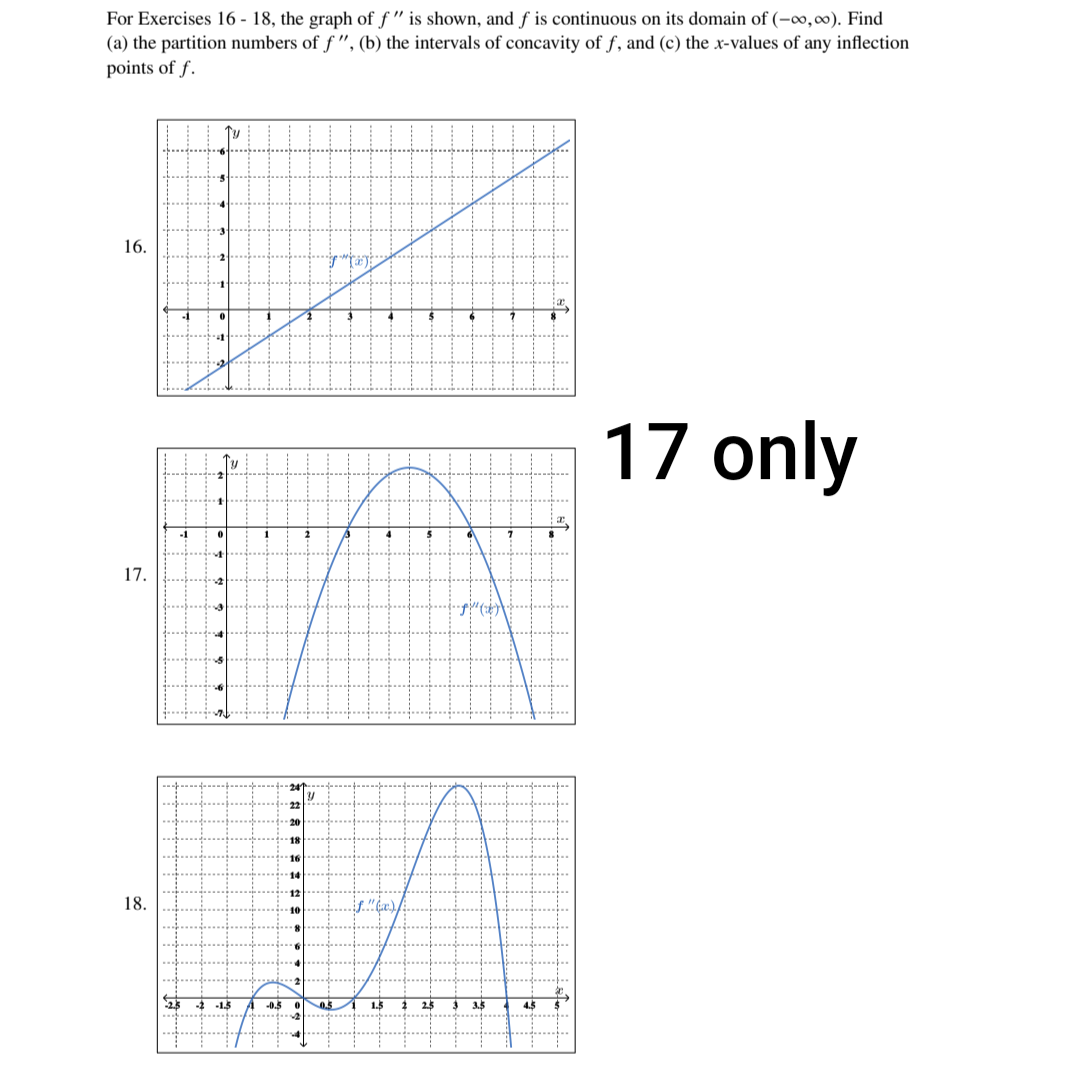
BASIC SKILLS PRACTICE For Exercises 1 - 6, find f"(x). 1. f(x) = 7x3+8 In(x)-x-x-5 1 and 5 2. f(x) = (2x + 13)9 3. f(x) = e'+ 4 2 -21 4 . f' ( x ) = @5x+9 5. f'(x) =x44-0.3x12 + Vx-x-4/5 6. f' (x) = In(8x3-22)For Exercises 10 - 12, f" and the domain of f are given. Assuming f is continuous on its domain, find (a) the partition numbers of , (b) the intervals of concavity of f, and (c) the x-values of any inflection points of f using the Concavity Test. 10. f"(x) = (x+6)*(x=3)(x=7); domain of f is (c0,0) 11 f"(x) =2x(x+4)(x8)'; domain of f is (c0,c0) 3(x10)(x+2) 12. f"(x)= T domain of f is (=0, =5)U(=5,00) For Exercises 13 - 15, find (a) the partition numbers of f ", (b) the intervals of concavity of f, and (c) any inflection points of f using the Concavity Test. 11 and 15 14. f(x) =4x> +24x2 =384x+3 15. f(x) = x* 54x2 For Exercises 16 - 18, the graph of " is shown, and f is continuous on its domain of (co,c0). Find (a) the partition numbers of f\For Exercises 22 - 26, the domain of f is (co,c0), and f is twice-differentiable on its domain. Use the Second Derivative Test, if possible, to classify whether f has a local minimum, local maximum, or neither at the indicated x-value. If it is not possible, explain why. 22. x=1, f'(1)=0,and f\"(1)=9 23. x=-8, f'(-8)=0,and f ""(-8) = -13 24. x=14, f'(14)=0,and f\"(14) = -7.93 25. x=12.5, f'(12.5)=0, and f "'(12.5) = 827 26. x=-127, f'(-127)=0,and f \"(=127) = e INTERMEDIATE SKILLS PRACTICE 2., For Exercises 27 - 31, find i'.-;- dx- v 25,27 and 33 28. y = xe* 4 X 29, y= Y= +1a 30. y =log,(8x+5)10x 31, y=13H For Exercises 32 - 37, find (a) the intervals of concavity and (b) any inflection points of f. 2x-18 i i