Bayesian coin flip. Let us try out another prior for the Bayesian coin flip problem that we discussed in class. We now model the parameter of the Bernouilli as being uniform between 1/2 and 1.

1. Briefly justify the model and compute the probability that the result of the coin flip is heads or tails under this model.
2. After the coin flip we update the distribution of the bias of the coin (i.e. the parameter of the Bernouilli that represents the coin flip) by conditioning it on the outcome. Compute the distribution if the outcome is tails and if the outcome is heads. Sketch any distributions you compute and explain why the drawing makes sense.
3. Compare the prior distribution for the bias that we discussed in class and the one in this model. Which one is more restrictive and why?

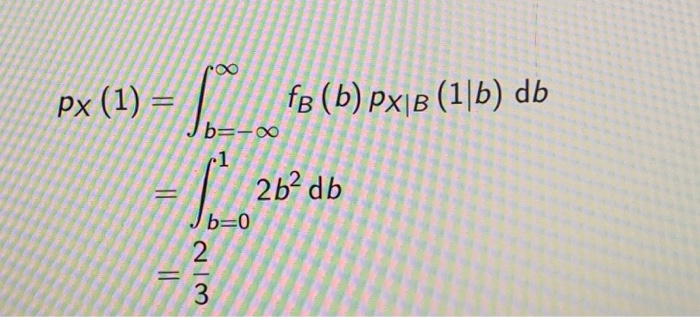
\f