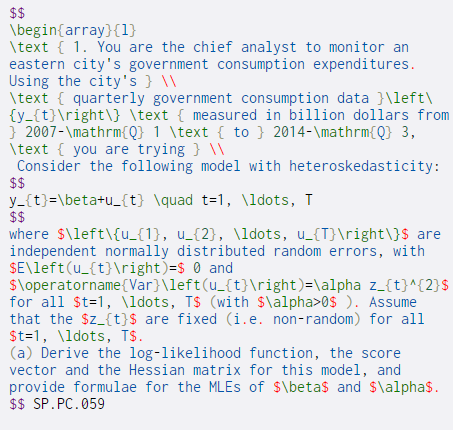
$$ \begin{array}{1} \text { 1. You are the chief analyst to monitor an eastern city's government consumption expenditures. Using the city's } \text { quarterly government consumption data }\left\ {y_{t} ight\} \text { measured in billion dollars from } 2007-\mathrm{Q} 1 \text { to } 2014-\mathrm{Q} 3, \text { you are trying } \ Consider the following model with heteroskedasticity: $$ y_{t}=\beta+u_{t} \quad t=1, \ldots, I $$ where $\left\{u_{1}, u_{2}, \ldots, u_{T} ight\}$ are independent normally distributed random errors, with $E\left(u_{t} ight) =$ 0 and $\operatorname {Var}\left(u_{t} ight)=\alpha z_{t}^{2}$ for all $t=1, \ldots, T$ (with $\alpha>0$ ). Assume that the $z_{t}$ are fixed (i.e. non-random) for all $t=1, \ldots, T$. (a) Derive the log-likelihood function, the score vector and the Hessian matrix for this model, and provide formulae for the MLEs of $\beta$ and $\alpha$. $$ SP.PC.059