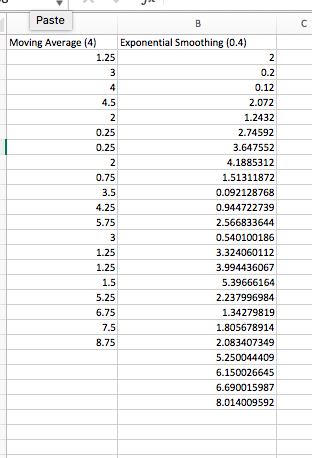
\begin{tabular}{|c|c|} \hline Paste & B \\ \hline Moving Average (4) & Exponential Smoothing (0.4) \\ \hline 1.25 & 2 \\ \hline 3 & 0.2 \\ \hline 4 & 0.12 \\ \hline 4.5 & 2.072 \\ \hline 2 & 1.2432 \\ \hline 0.25 & 2.74592 \\ \hline 0.25 & 3.647552 \\ \hline 2 & 4.1885312 \\ \hline 0.75 & 1.51311872 \\ \hline 3.5 & 0.092128768 \\ \hline 4.25 & 0.944722739 \\ \hline 5.75 & 2.566833644 \\ \hline 3 & 0.540100186 \\ \hline 1.25 & 3.324060112 \\ \hline 1.25 & 3.994436067 \\ \hline 1.5 & 5.39666164 \\ \hline 5.25 & 2.237996984 \\ \hline 6.75 & 1.34279819 \\ \hline 7.5 & 1.805678914 \\ \hline \multirow[t]{8}{*}{8.75} & 2.083407349 \\ \hline & 5.250044409 \\ \hline & 6.150026645 \\ \hline & 6.690015987 \\ \hline & 8.014009592 \\ \hline & \\ \hline & \\ \hline & \\ \hline \end{tabular} Which of the following is true about the number of absolute forecast errors for the moving average approach with a window of 4 (Column A ) and exponential smoothing with a smoothing constant of 0.4 (Column B)? There isn't enough information provided to answer this question. The moving average approach has more absolute forecast errors. The exponential smoothing approach has more absolute forecast errors. The two columns have the same number of absolute forecast errors. Question 7 (10 points) How many of the absolute forecast errors under the exponential smoothing approach are greater than 5 ? 2 5 12 1