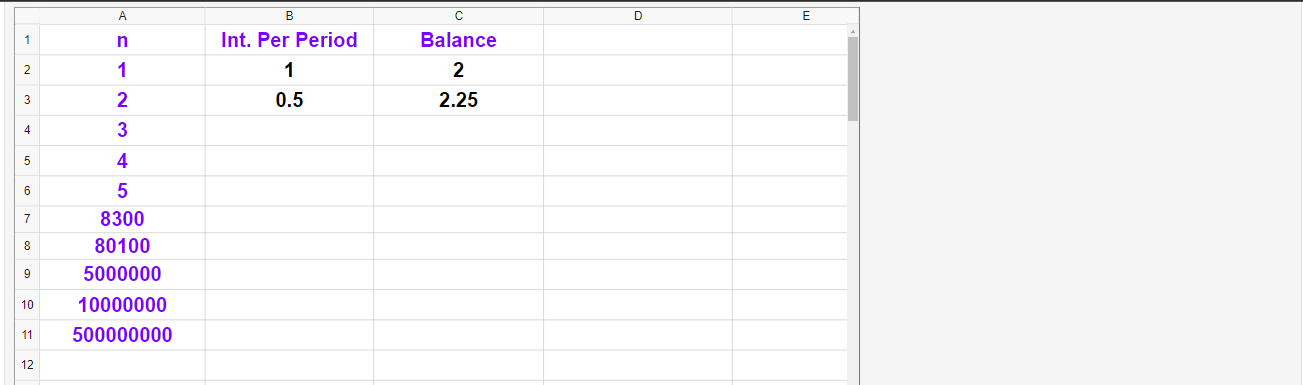
\begin{tabular}{|c|c|c|c|c|c|} \hline & A & B & C & D \\ \hline 1 & n & Int. Per Period & Balance & \\ \hline 2 & 1 & 1 & 2 & \\ \hline 3 & 2 & 0.5 & 2.25 \\ \hline 4 & 3 & & \\ \hline 5 & 4 & & \\ \hline 6 & 5 & & \\ \hline 7 & 8300 & & \\ \hline 8 & 80100 & & \\ \hline 9 & 5000000 & & \\ \hline 10 & 10000000 & & & \\ \hline 11 & 500000000 & & & \\ \hline 12 & & & & \\ \hline \end{tabular} \begin{tabular}{|l|c|c|c|} \hline 15 & & & \\ \hline 16 & n & Int. Per Period & Balance \\ \hline 17 & 1 & 0.183 & 1.183 \\ \hline 18 & 2 & 0.0915 & 1.19137225 \\ \hline 19 & 3 & & \\ \hline 20 & 8300 & & \\ \hline 21 & 80100 & & \\ \hline 22 & 5000000 & & \\ \hline 23 & 10000000 & & \\ \hline 24 & 500000000 & & \\ \hline 25 & & & \\ \hline 26 & & & \\ \hline \end{tabular} ADTF Distributors is opening a corporate office building in Kansas, near the campus of CLU. They contact the business college at CLU to solicit applications from students for consideration for several openings in the Finance division at the new site. Applicants invited to the first round of interviews were asked to use the block of cells A1-C11 in the above spreadsheet applet. These cells are programmed to display data for a scenario where $1 is invested at 100% interest compounded n times per year. Column A gives possible values for the number of compounding periods and Column C gives the balance at the end of 1 year. Note: There are formulas entered in Columns B and C of row 3 . If you delete the data in these cells, you can refresh the applet (or reload the page) to restore them. If you grab the lower right comer of a cell with a formula, you can drag the formula to fill down the column. For example, you could do this with cell B3. See how well you would perform at the first round of interviews by completing the exercises below. INTERVIEW - ROUND ONE (a) Let n stand for the number of compounding periods. Then, using the compound interest formula, the future value when $1 is invested at 100% interest for 1 year will be (1+/() This simplifies to (1+n1)n (b) Suppose that interest is compounded 8300 times per year (see row 7 in the applet). Then, we may conclude that when $ is invested at % interest compounded times per year, the balance at the end of one year will be $ (round to 5 decimal places). In other words, (c) Suppose that interest is compounded 80100 times per year (see row 8 in the applet). Then, we may conclude that when $ is invested at % interest compounded times per year, the balance at the end of one year will be $ (round to 6 decimal places). In other words, (1+/)80100 (d) Column A is used to investigate what happens as you let the number of compounding periods increase without bound. In other words, to mimic what happens as we let n. Because we cannot use as a number of compounding periods, we refer to this type of compounding (when n ) as continuous compounding. Looking at the values down Column C, it appears that the balance at the end of 1 year at 100% interest compounded continuously (rounded to the nearest cent) is $ which means the account earned $ in interest. (e) Correct to 5 decimal places, it appears that as n, (1+n1)n INTERVIEW - ROUND TWO cell with a formula, you can drag the formula to fill down the column. For example, you could do this with cell B18 into B19. (f) Let n stand for the number of compounding periods. Then, using the compound interest formula, the future value when $1 is invested at 18.3% interest for 1 year will be (1+/)(. This simplifies to (1+n0.183)n (g) Suppose that interest is compounded 8300 times per year (see row 20 in the applet). Then, we may conclude that when $ is invested at % interest compounded times per year, the balance at the end of one year will be $ (round to 5 decimal places). In other words, (h) Suppose that interest is compounded 80100 times per year (see row 21 in the applet). Then, we may conclude that when $ is invested at % interest compounded times per year, the balance at the end of one year will be $ (round to 6 decimal places). In other words, (1+/)80100 1 year at 18.3% interest compounded continuously (rounded to the nearest cent) is $ , which means the account earned $ in interest. (j) Correct to 5 decimal places, it appears that as n, (1+n0.183)n ADTF Distributors