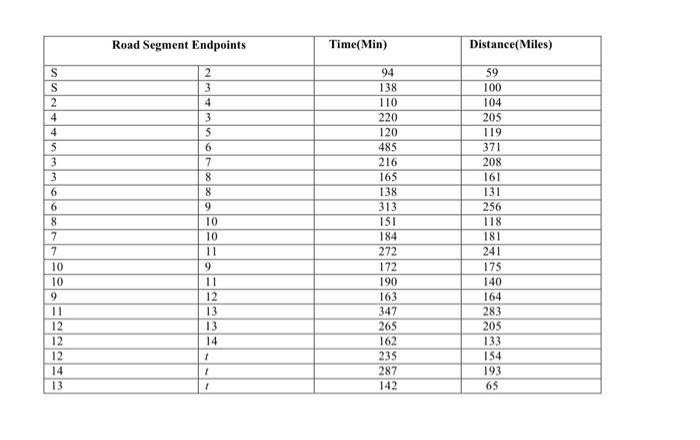
Question: begin{tabular}{|l|l|c|c|} hline multicolumn{2}{|c|}{ Road Segment Endpoints } & Time(Min) & Distance(Miles) hline S & 2 & 94 & 59 hline S & 3


Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


