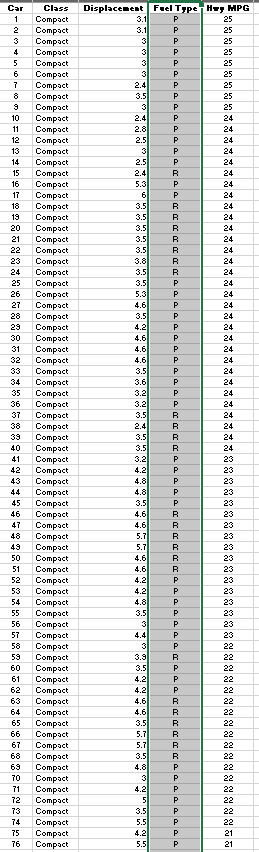
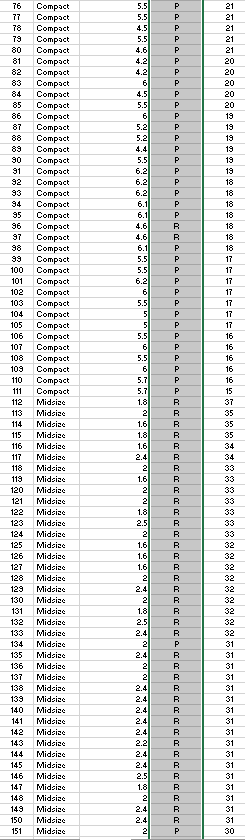
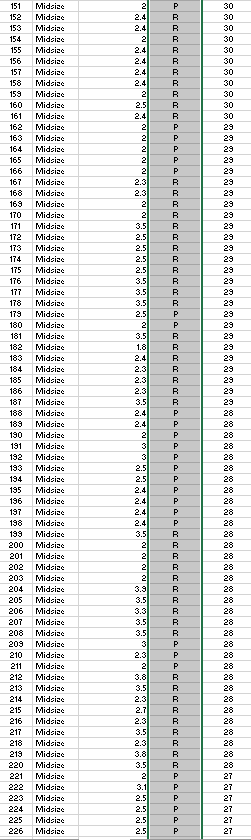
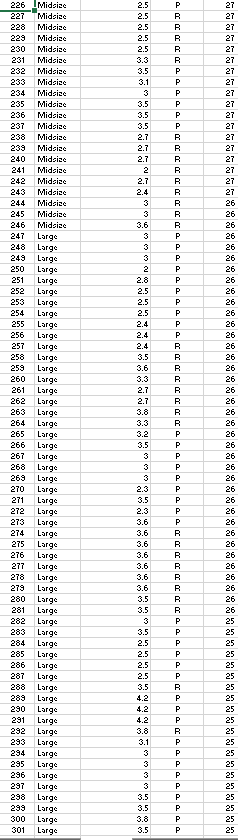
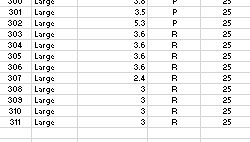
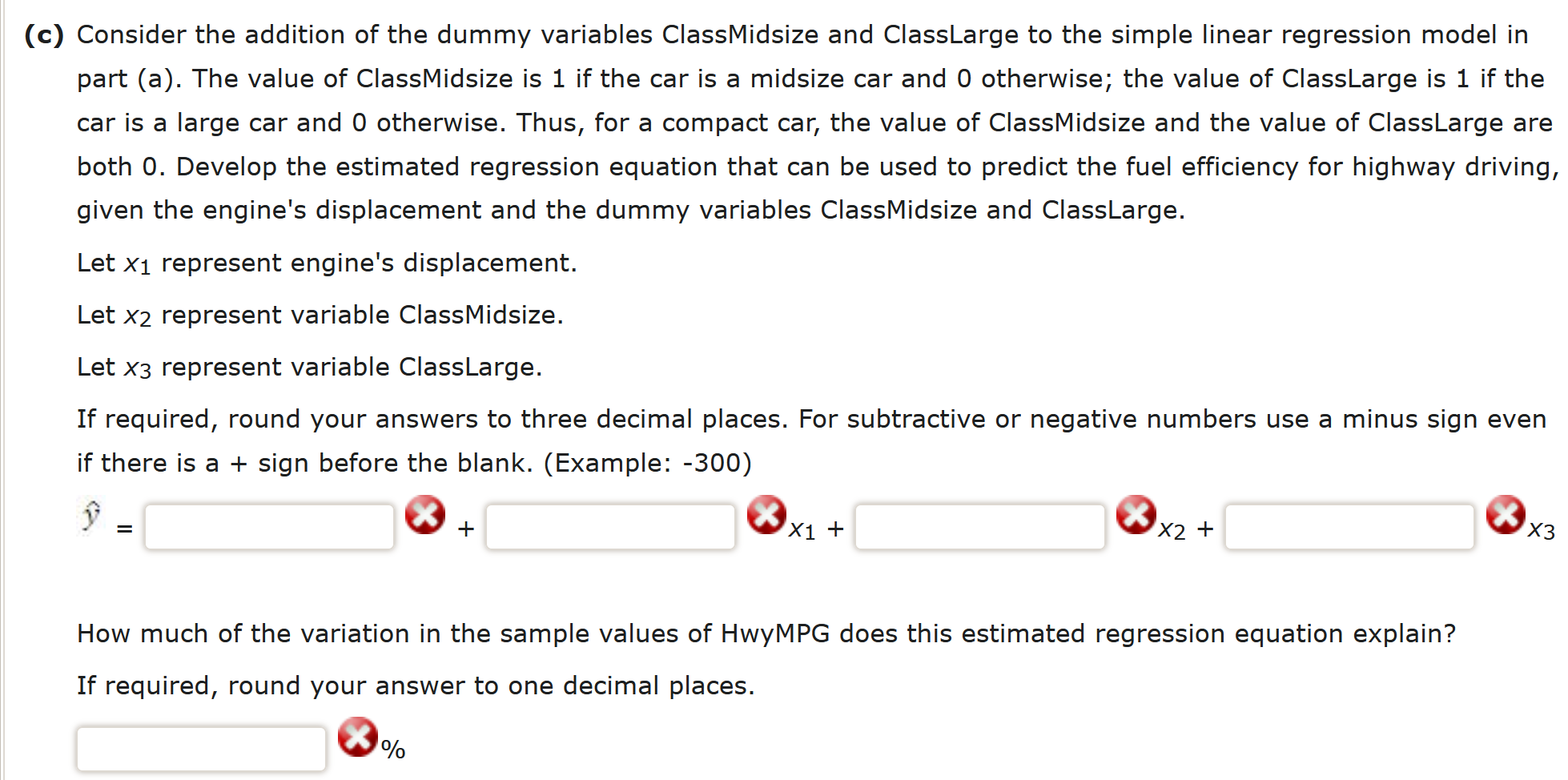
\begin{tabular}{|l|l|l|l|l|} \hline 3001 & Large & 3.5 & P & 25 \\ \hline 302 & Large & 5.3 & P & 25 \\ \hline 303 & Large & 3.6 & R & 25 \\ \hline 304 & Large & 3.6 & R & 25 \\ \hline 305 & Large & 3.6 & R & 25 \\ \hline 306 & Large & 3.6 & R & 25 \\ \hline 307 & Large & 2.4 & R & 25 \\ \hline 306 & Large & 3 & R & 25 \\ \hline 309 & Large & 3 & R & 25 \\ \hline 310 & Large & 3 & R & 25 \\ \hline 311 & Large & 3 & R & 25 \\ \hline \end{tabular} c) Consider the addition of the dummy variables ClassMidsize and ClassLarge to the simple linear regression model in part (a). The value of ClassMidsize is 1 if the car is a midsize car and 0 otherwise; the value of ClassLarge is 1 if the car is a large car and 0 otherwise. Thus, for a compact car, the value of ClassMidsize and the value of ClassLarge are both 0 . Develop the estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement and the dummy variables ClassMidsize and ClassLarge. Let x1 represent engine's displacement. Let x2 represent variable ClassMidsize. Let x3 represent variable ClassLarge. If required, round your answers to three decimal places. For subtractive or negative numbers use a minus sign even if there is a+ sign before the blank. (Example: -300 ) y^= How much of the variation in the sample values of HwyMPG does this estimated regression equation explain? If required, round your answer to one decimal places. % ) Consider the addition of the dummy variable FuelPremium, where the value of FuelPremium is 1 if the car uses premium fuel and 0 if the car uses regular fuel. Develop the estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement, the dummy variables ClassMidsize and ClassLarge, and the dummy variable FuelPremium. Let x1 represents engine's displacement. Let x2 represents variable ClassMidsize. Let x3 represents variable ClassLarge. Let x4 represents variable FuelPremium. If required, round your answers to three decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300 ) How much of the variation in the sample values of HwyMPG does this estimated regression equation explain? If required, round your answer to one decimal places. % \begin{tabular}{|l|l|l|l|l|} \hline 3001 & Large & 3.5 & P & 25 \\ \hline 302 & Large & 5.3 & P & 25 \\ \hline 303 & Large & 3.6 & R & 25 \\ \hline 304 & Large & 3.6 & R & 25 \\ \hline 305 & Large & 3.6 & R & 25 \\ \hline 306 & Large & 3.6 & R & 25 \\ \hline 307 & Large & 2.4 & R & 25 \\ \hline 306 & Large & 3 & R & 25 \\ \hline 309 & Large & 3 & R & 25 \\ \hline 310 & Large & 3 & R & 25 \\ \hline 311 & Large & 3 & R & 25 \\ \hline \end{tabular} c) Consider the addition of the dummy variables ClassMidsize and ClassLarge to the simple linear regression model in part (a). The value of ClassMidsize is 1 if the car is a midsize car and 0 otherwise; the value of ClassLarge is 1 if the car is a large car and 0 otherwise. Thus, for a compact car, the value of ClassMidsize and the value of ClassLarge are both 0 . Develop the estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement and the dummy variables ClassMidsize and ClassLarge. Let x1 represent engine's displacement. Let x2 represent variable ClassMidsize. Let x3 represent variable ClassLarge. If required, round your answers to three decimal places. For subtractive or negative numbers use a minus sign even if there is a+ sign before the blank. (Example: -300 ) y^= How much of the variation in the sample values of HwyMPG does this estimated regression equation explain? If required, round your answer to one decimal places. % ) Consider the addition of the dummy variable FuelPremium, where the value of FuelPremium is 1 if the car uses premium fuel and 0 if the car uses regular fuel. Develop the estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement, the dummy variables ClassMidsize and ClassLarge, and the dummy variable FuelPremium. Let x1 represents engine's displacement. Let x2 represents variable ClassMidsize. Let x3 represents variable ClassLarge. Let x4 represents variable FuelPremium. If required, round your answers to three decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300 ) How much of the variation in the sample values of HwyMPG does this estimated regression equation explain? If required, round your answer to one decimal places. %