Below is a step-by-step procedure in solving the mean and variance of a sampling

distribution of a sample means involving the mean and variance of a discrete

random variable, which is already answered for you. Your job is to check for errors

in each step of the solution. If there are errors, do the following in the table after

the test sample and write the answers on a separate sheet of paper:

1. Identify the errors.

2. Correct the errors.

3. Then explain why your correction is right.

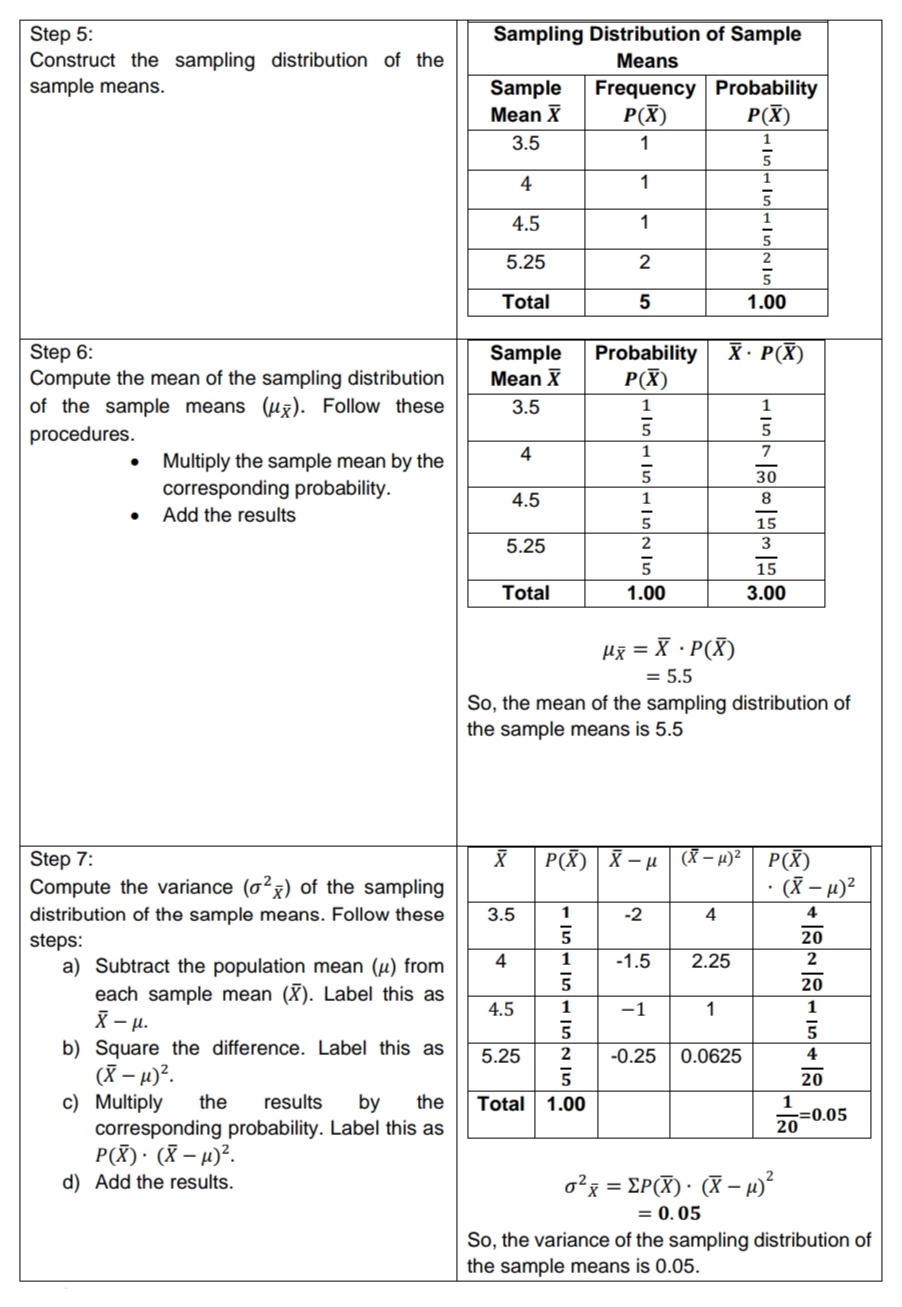
Step 1: EX N 1+3+4+6+8 = 4 = 5.5 So, the mean of the population is 5.5 Step 2: X X - u ( X - 1) 2 1 -4.5 20.25 3 -2.5 6.25 4 -1.5 2.25 6 0.5 0.25 8 2.5 6.25 E(X - 1)2 =35.25 35.25 62 = E(X - () 2 = N 4 = 8.81 So, the variance of the population is 5.84 Step 3 Determine the number of possible samples of | Use the formula NCn. size n =4 Here, N = 5 and n = 4 5C4 = 5 So, there are 5 possible samples of size 4 that can be drawn. Step 4: Samples Mean List all possible samples and their 1, 3, 4, 6 3.5 corresponding means. 1, 3, 4, 8 4 1, 3, 6, 8 4.5 1, 3, 4, 8 4 3, 4, 6, 8 5.25Step 5: Sampling Distribution of Sample Construct the sampling distribution of the Means sample means. Sample Frequency Probability Mean X P(X) P(X) 3.5 4 4.5 5.25 2 Total 5 1.00 Step 6: Sample Probability X . P(X) Compute the mean of the sampling distribution Mean X P(X) of the sample means (ux). Follow these 3.5 procedures. . Multiply the sample mean by the 4 corresponding probability. 4.5 . Add the results 5.25 15 Total 1.00 3.00 Hx = X . P(X) = 5.5 So, the mean of the sampling distribution of the sample means is 5.5 Step 7: X P(X) X - H (X-1) 2 P(X) Compute the variance ( x) of the sampling . ( X - 1) 2 distribution of the sample means. Follow these 3.5 -2 4 steps: 20 a) Subtract the population mean (u) from 4 -1.5 2.25 20 each sample mean (X). Label this as 4.5 -1 X - H. b) Square the difference. Label this as 5.25 -0.25 0.0625 ( X - 1 ) 2. c) Multiply the results by the Total 1.00 1 corresponding probability. Label this as 20 -=0.05 P (X ) . ( X - 1) 2. d) Add the results. 02 x = EP ( X) . ( X - 1)2 = 0. 05 So, the variance of the sampling distribution of the sample means is 0.05